考虑风电出力随机特性的氢储能综合能源系统优化调度

引用本文

黄涛, 许志鹏, 葛乐. 考虑风电出力随机特性的氢储能综合能源系统优化调度[J]. 电器与能效管理技术, 2020(5): 72-77.
HUANG Tao, XU Zhipeng, GE Le. Optimal Scheduling of Hydrogen Energy Storage System Considering Random Characteristics of Wind Power Output[J]. ELECTRICAL & ENERGY MANAGEMENT TECHNOLOGY, 2020(5): 72-77.
Doi:10.16628/j.cnki.2095-8188.2020.05.012 复制到剪切板

Permissions

《电器与能效管理技术》编辑部所有

考虑风电出力随机特性的氢储能综合能源系统优化调度

黄涛¹, 许志鹏², 葛乐²

1.江苏方天电力技术有限公司, 江苏南京 211100

2.南京工程学院, 江苏南京 211167

作者简介：

黄涛(1990—),男,工程师,硕士,主要从事电气设备高压试验与故障诊断。
许志鹏(1993—),男,硕士研究生,研究方向为综合能源系统。
葛乐(1982—),男,副教授,研究方向为新能源与主动配电网。

收稿日期: 2019-12-21

摘要

基于含大规模风电氢储能综合能源系统,提出了一种以系统运行成本最低为目标,考虑风能不确定性、随机安全约束机组组合和需求响应的日前优化模型。在改进的6节点系统和24节点系统上进行算例分析。结果表明,同时考虑氢储能综合能源系统和需求响应对电力调度的影响,弃风量和日运营成本均有所降低。

关键词: 氢储能; 需求响应; 风能; 综合能源系统; 机组组合; 安全约束

中图分类号:TM734 文献标志码:A 文章编号:2095-8188(2020)05-0072-06 doi: 10.16628/j.cnki.2095-8188.2020.05.012

Optimal Scheduling of Hydrogen Energy Storage System Considering Random Characteristics of Wind Power Output

HUANG Tao¹, XU Zhipeng², GE Le²

1. Jiangsu Fangtian Power Technology Co.,Ltd., Nanjing 211100, China

2. Nanjing Institute of Technology, Nanjing 211167, China

Abstract

Based on the hydrogen energy storage system (HESS) with large scale wind power,a pre-optimization model to minimize system operation cost considering wind energy uncertainty,stochastic safety constraint unit combination and demand response was proposed.The results of an improved 6-bus system and a 24-bus system show that if the impact of both hydrogen energy storage integrated energy system and demand response on power dispatching is considered,the amount of abandoned air and daily operating costs are reduced.

Keyword: hydrogen energy storage; demand response; wind energy; integrated energy system; unit combination; safety constraint

文章图片

0 引言

随着社会对能源安全、生态环境、气候异常等问题的日益重视, 减少化石能源燃烧, 加快开发和利用可再生能源已成为世界各国的普遍共识。根据国家能源局数据显示, 2017年我国风力发电量达到3 057亿kWh, 同比增长26.3%, 弃风率为12%。因此, 增加可再生能源的渗透率^{[1, 2]}对电力生产和消费之间的平衡提出了新的挑战。

为了应对这些挑战, 近些年提出了灵活调节服务^[3]、需求响应(Demand Response, DR)与风能的协调^{[4, 5]}、能源存储系统与风电场的协调运行^[6]等方法来解决清洁能源消纳问题。DR规划在电力系统^[7]和电力市场^[8]可靠经济运行中发挥着重要作用。通过执行DR程序, 用户在负荷高峰或短缺风电时减少用电量, 并在负荷低谷或风电溢出时增加用电量。因此, DR可以影响电价, 减少高峰负荷, 减少弃风, 并节约系统运营成本^{[9, 10]}。DR主要分为激励型需求响应(Incentive-based Demand Response, IDR)和价格型需求响应(Price-based Demand Response, PDR)两大类。IDR是指DR实施者根据电网供需状况制定相应政策, 用户在系统需要或电力紧张时减少用电需求, 并获得直接补偿或在其他时段获得优惠电价的响应方式; PDR是指用户收到价格信号后, 相应调整其用电需求, 从而达到改变负荷曲线的目的。文献[4]研究了DR与风能协调对电力系统运行成本和弃风率的影响。文献[11]提出了基于DR和风、光发电机组与燃气轮机冷热电联产(Combined Cooling, Heating and Power, CCHP)系统结合的优化调度方法, 有效降低了系统综合运行成本。文献[12]提出了一种基于偏差预控的负荷调度模式, 构建了多时间尺度滚动调度计划模型来实现风电和DR在不同时间尺度上的协调优化。文献[13]在考虑综合成本的前提下, 兼顾风电预测和PDR二者的不确定性以及系统安全约束, 构建了基于光热电站和PDR参与风电消纳的调度模型。在接入大规模风电的情况下, 风电出力的不确定性不可避免地对电力系统安全经济运行造成影响^[14]。文献[15]考虑了风电不确定性对电力系统运行调度的影响, 提出了基于风电区间预测信息的随机安全约束机组组合模型。文献[16]针对大规模风电并网影响电网稳定运行的问题, 提出了最小化风电-抽水蓄能联合系统发电成本模型。

本文旨在优化含大规模风电的氢储能综合能源系统(Hydrogen Energy Storage System, HESS)的经济性并提高清洁能源消纳。重点基于风电不确定性、需求响应和随机安全约束机组组合(Stochastic Security-Constrained Unit Commitment, SSCUC)的氢储能综合能源系统进行建模, 构建以运营成本最低和弃风量最少为目标的优化调度模型, 并转化为确定的方程进行求解。

1 HESS

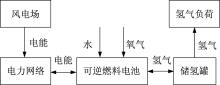
HESS结构如图1所示。在HESS中, 由可再生能源产生的过剩功率通过可逆固体氧化物燃料电池(Reversible Solid Oxide Fuel Cell, RSOFC)^[17]中的固体氧化物电解池(Solid Oxide Electrolytic Cell, SOEC)电解转化为氢(Power to Hydrogen, P2H), 并存储在储氢罐中。然后, 在用电高峰或风力发电短缺时, 将储氢罐中氢气通过RSOFC中的固体氧化物燃料电池(Solid Oxide Fuel Cell, SOFC)转换为电力(Hydrogen to Power, H2P)。HESS相对于其他储能系统的主要特征是存储的氢可用于氢依赖性工业或注入天然气网络以供消费者使用。

	Figure Option View Download New Window
	图1 HESS结构系统

目前, 电解制氢技术较为成熟, 主要可以分为以下3种技术:①碱性电解槽制氢, 但制氢效率低、能耗大, 且存在渗碱的环境污染问题; ②质子交换膜制氢, 电极多用贵重金属铂, 成本高, 难以大规模应用; ③可逆固体氧化物燃料电池制氢, 效率高, 电解效率可达90%以上。2017年9月8日河北沽源县境内建设的全球最大、国内首个风电制氢综合利用示范项目全部并网发电^[18]。

本文主要围绕可逆固体氧化物燃料电池和DR对HESS调度和风电消纳的影响进行研究。

2 HESS模型建立

2.1 目标函数

以系统运营成本最低为目标, 构建HESS模型:

$\min \overset{N_{S}}{\sum_{s = 1}} π_{s} [F_{d} + F_{i} + 2 F_{h}^{P 2 H}]$ （1）

式中: N_S— — 场景总数;

π _s— — 场景s的概率;

F_d— — 实行DR的成本;

F_i— — 火电机组的发电费用;

$F_{h}^{P 2 H}$ 、 $F_{h}^{H 2 P}$ — — RSOFC在SOEC和SOFC状态下HESS的成本。

DR成本为

$F_{d} = \overset{N_{T}}{\sum_{t = 1}} \overset{N_{D}}{\sum_{d = 1}} B_{d, t} P_{d, t, s}^{PBL}$ （2）

式中: N_T— — 调度时段;

N_D— — 负载个数;

B_d_,_t— — 第d个负载t时段实行DR的补偿电价;

$P_{d, t, s}^{PBL}$ — — s场景下t时段的售电功率。

火电机组成本为

$F_{i} = \overset{N_{T}}{\sum_{t = 1}} \overset{N_{U}}{\sum_{i = 1}} (a_{i} P_{i, t, s}^{2} + b_{i} P_{i, t, s} + c_{i})$ （3）

式中: N_U— — 火电机组个数;

a_i、b_i、c_i— — 火电机组的发电费用系数。

HESS成本为

$F_{h}^{P 2 H} = F_{h}^{H 2 P} = \overset{N_{T}}{\sum_{t = 1}} \overset{N_{H}}{\sum_{h = 1}} (b_{h}^{P 2 H} P_{h, t, s}^{P 2 H} + c_{h}^{P 2 H})$ （4）

式中: NH— — RSOFC组数目;

$b_{h}^{P 2 H}$ 、 $c_{h}^{P 2 H}$ — — RSOFC组的成本系数, 且假设SOFC状态下HESS具有和SOEC状态下相同的成本函数。

2.2 电力系统约束

(1)机组出力约束:

$P_{i}^{\min} I_{i, t, s} \leq P_{i, t, s} \leq P_{i}^{\max} I_{i, t, s}$ （5）

式中: $P_{i}^{\max}$ 、 $P_{i}^{\min}$ — — 第i组火电机组出力上、下限;

P_i_,_t_,_s— — s场景下第i组火电机组在t时段的出力;

I_i_,_t_,_s— — s场景下第i组火电机组在t时段运行情况, 分别用1和0表示运行和停机状态。

(2) 机组爬坡约束:

$P_{i, dn}^{\min} \leq P_{i, t, s} - P_{i, t - 1, s} \leq P_{i, up}^{\max}$ （6）

式中: $P_{i, up}^{\max}$ 、 $P_{i, dn}^{\min}$ — — 第i组火电机组在t时段的最大爬坡上限和最小爬坡下限。

(3)系统安全的旋转备用约束:

$\{\begin{array}{l} \overset{N_{U}}{\sum_{i = 1}} (P_{i, t, s}^{\max} - P_{i, t, s}) \geq R_{t, up} \\ \overset{N_{U}}{\sum_{i = 1}} (P_{i, t, s} - P_{i, t, s}^{\min}) \geq R_{t, dn} \end{array}$ （7）

式中: $P_{i, t, s}^{\max}$ 、 $P_{i, t, s}^{\min}$ — — s场景下第i组火电机组在t时段最大可用出力和最小可用出力;

R_t_{, up}、R_t_{, dn}— — 系统安全的正旋转和负旋转备用。

(4) 风电约束:

$0 \leq P_{w, t, s} \leq P_{w, t, s}^{\max}$ （8）

式中: P_w_,_t_,_s— — s场景下t时段风电出力实际值;

$P_{w, t, s}^{\max}$ — — s场景下t时段最大风电出力。

风力发电预测误差可以通过正态分布函数来表示为

$f_{PDF} (ε) = \frac{1}{\sqrt[]{2 π σ^{2}}} e^{- \frac{1}{2} {(\frac{ε - ε_{0}}{σ})}^{2}}, - \infty \leq ε \leq \infty$ （9）

式中: f_PDF(ε )— — 用正态分布概率分布函数表示的风力发电预测误差。

(5) DR模型。DR模型将负载分为基本负荷(Base Load, BL)和电价型负荷(Price-Based Load, PBL)。BL对价格变化不敏感, 并根据历史数据预测; 而PBL根据电价变化调整其运行状态。

$P_{d, t, s}^{PBL} = {P^{E}}_{d, t} - P_{d, t, s}^{BL} - P_{d, t}^{BL}$ （10）

$0 \leq P_{d, t, s}^{PBL} \leq P_{d, t, s}^{\max}$ （11）

$|P_{d, t, s}^{BL}| \leq P_{d, t, \max}^{BL}$ （12）

$\overset{N_{T}}{\sum_{t = 1}} P_{d, t, s}^{BL} = 0$ （13）

式中: ${P^{E}}_{d, t}$ — — 用电负荷在t时段预测值;

$P_{d, t}^{BL}$ — — t时段固定负荷;

$P_{d, t, s}^{BL}$ — — s场景下t时段可调负荷;

$P_{d, t, s}^{PBL}$ — — s场景下t时段电价激励型负荷。

(6) 功率平衡约束。每个总线的功率平衡方程可表示为

$\begin{array}{l} \overset{N_{U_{b}}}{\sum_{i = 1}} P_{i, t, s} + \overset{N_{W_{b}}}{\sum_{w = 1}} P_{w, t, s} + \overset{N_{H_{b}}}{\sum_{h = 1}} P_{h, t, s}^{H 2 P} - \\ \overset{N_{H_{b}}}{\sum_{h = 1}} P_{h, t, s}^{P 2 H} - \overset{N_{D_{b}}}{\sum_{d = 1}} ({P^{E}}_{d, t} - P_{d, t, s}^{BL}) = \overset{N_{L_{b}}}{\sum_{L = 1}} P_{L, t, s} \end{array}$ （14）

式中: $N_{U_{b}}$ — — 火电机组在总线b处的数量;

N_wb— — 风电机组在总线b处的数量;

$N_{D_{b}}$ — — 需求响应负载的数量;

$N_{H_{b}}$ — — 可逆燃料电池在总线b处的数量;

P_L_,_t_,_s— — 电力系统线路L在s场景下t时段功率潮流。

从总线b到总线b'的功率传输约束表示为

$P_{L, t, s} = \frac{δ_{b, t, s} - δ_{b', t, s}}{X_{L}}$ （15）

式中: δ _b_,_t_,_s— — 总线路b在场景s下t时段的电压相角;

X_L— — 总线L的阻抗。

(7) 功率传输约束:

$- P_{L}^{\max} \leq P_{L, t, s} \leq P_{L}^{\max}$ （16）

式中: $P_{L}^{\max}$ — — 电力系统线路L最大功率潮流上限。

2.3 HESS模型

(1) RSOFC约束:

$\{\begin{array}{l} P_{h, \min}^{P 2 H} I_{h, t, s}^{P 2 H} \leq P_{h, t, s}^{P 2 H} \leq P_{h, \max}^{P 2 H} I_{h, t, s}^{P 2 H} \\ P_{h, \min}^{H 2 P} I_{h, t, s}^{H 2 P} \leq P_{h, t, s}^{H 2 P} \leq P_{h, \max}^{H 2 P} I_{h, t, s}^{H 2 P} \\ I_{h, t, s}^{H 2 P} + I_{h, t, s}^{P 2 H} \leq 1 \end{array}$ （17）

式中: $P_{h, \min}^{P 2 H}$ 、 $P_{h, \max}^{P 2 H}$ — — SOEC工作状态中RSOFC最小转换功率和最大转换功率;

$P_{h, \max}^{H 2 P}$ 、 $P_{h, \min}^{H 2 P}$ — — SOFC工作状态中RSOFC最大转换功率和最小转换功率;

$P_{h, t, s}^{P 2 H}$ 、 $P_{h, t, s}^{H 2 P}$ — — SOEC和SOFC工作状态中s场景下RSOFC在t时段转换功率;

$I_{h, t, s}^{P 2 H}$ 、 $I_{h, t, s}^{H 2 P}$ — — SOEC和SOFC工作状态中s场景下RSOFC在t时段运行状态。

(2) 储气设备约束:

$E_{h, t, s} = E_{h, t - 1, s} + η_{h}^{P 2 H} P_{h, t, s}^{P 2 H} I_{h, t, s}^{P 2 H} - \frac{P_{h, t, s}^{H 2 P}}{η_{h}^{H 2 P}} I_{h, t, s}^{H 2 P} - M_{h, t, s}$ （18）

$E_{h}^{\min} \leq E_{h, t, s} \leq E_{h}^{\max}$ （19）

$0 \leq M_{h, t, s} \leq M_{h, \max}$ （20）

式中: E_h_,_t_,_s— — 储气设备在s场景下t时段储气量;

$η_{h}^{P 2 H}$ 、 $η_{h}^{H 2 P}$ — — SOEC和SOFC工作状态中转换效率;

M_h_,_t_,_s— — 转化为一些其他类型能量的氢气量;

$E_{h}^{\min}$ 、 $E_{h}^{\max}$ — — 储气设备容量最小值和最大值。

2.4 求解方法

建立的数学模型属于混合整数非线性规划模型。求解平台为MATLAB R2016a, 利用工具箱调用高效成熟的Cplex商业求解器进行求解。

3 算例分析

3.1 6节点系统

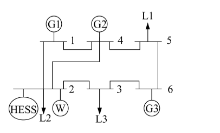
为了评估所提出的模型, 采用一种改进的6节点电力系统。综合能源系统结构图如图2所示。改进的6节点电力系统包括7条支路、3台火电机组、3个用电负荷、氢储能系统、风电厂。

	Figure Option View Download New Window
	图2 综合能源系统结构图

研究不同方案对弃风量和运营成本的影响:方案1解决SSCUC系统中火电的不确定性; 方案2解决SSCUC系统中风电的随机性; 方案3在SSCUC系统中整合HESS; 方案4在SSCUC系统中整合DR; 方案5在SSCUC系统中同时整合HESS和DR。

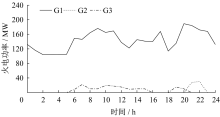
方案1:风力发电厂位于节点4上。火电机组G1、G2、G3出力如图3所示。其中, G1是3台机组中效率最高, 需要保持常开来满足实时功率平衡和系统经济性。G2(效率最低)和G3分别保证2 h和12 h的开机时间。这种情况下, 弃风量和运营成本分别为142.58 MWh和517 434.19元。

	Figure Option View Download New Window
	图3 火电机组G1、G2、G3的出力

方案2:设风力发电预测误差遵循正态分布, 预测值为均值, 标准差为5%。采用蒙特卡洛模拟风力发电的不确定性, 随机生成100个场景, 再通过K均值聚类法将100个场景缩减为5个场景。在不同场景中运营成本和弃风量如表1所示。场景4和场景5与前3个场景相比增加预测的风电出力, 结果运营成本降低, 弃风量增加。这种情况下, 预期的运营成本为517 627.6元, 弃风量为128.35 MWh。

表1 在不同场景中运营成本和弃风量

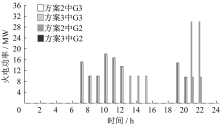
方案3:设HESS最大储氢容量为180 MWh, 最小储氢容量为40 MWh。储氢罐的初始值为最大值的40%, 并且储存的氢气只能通过RSOFC转换为电能。场景4下方案2和方案3中G2、G3的出力如图4所示。

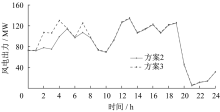
	Figure Option View Download New Window
	图4 场景4下方案2和方案3中G2、G3的出力

场景4下方案2和方案3中风电出力如图5所示。

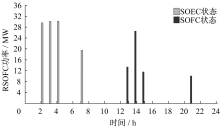
	Figure Option View Download New Window
	图5 场景4下方案2和方案3中风电出力

HESS在场景4下SOEC状态和SOFC状态的功率如图6所示。

	Figure Option View Download New Window
	图6 HESS在场景4下SOEC状态和SOFC状态的功率

HEES系统在第2、3、4、7小时存储多余的风力, 增加了风电出力。此外, 在第13、14、15和21小时, HESS在SOFC工作状态下工作, 向网络输送电力, 此时单火电机组G2和G3的出力减少。在这种情况下, 运营成本为503 063.68元, 弃风量为39.953 MWh, 低于方案2。

方案4:在系统中整合DR。DR参与因数(定义为可用DR与预期负载的比率)固定为0.03, 边际收益为315元/MWh。此时, 总运营成本为493 030.86元, 低于方案2和方案3; 而弃风量为103.31 MWh, 与方案3相比较高。为了充分评估每小时DR对电力系统运行成本和弃风量的影响, 认为DR参与因数为1%~4%。不同参与因数下运营成本和弃风量如表2所示。通过增加DR参与因数, 降低日常运行成本和弃风量。

表2 不同参与因数下的运营成本和弃风量

方案5:在这种情况下, 同时考虑DR和HESS。DR参与因数固定为0.03, HESS的规格与方案3相同。不同方案中运营成本和弃风量如表3所示。方案5弃风量为27.997 MWh, 运营成本为484 003.94元, 与之前的情况相比, 显著减少。

表3 不同方案中运营成本和弃风量

3.2 24节点系统

为研究HESS和DR对弃风量和运行成本的影响, 主要考虑4种方案:方案1解决SSCUC系统中风电的随机性; 方案2系统中只考虑DR; 方案3系统中只考虑HESS; 方案4系统中同时加入HESS和DR。

方案1中风电场位于节点6, 解决风电的随机性。在不考虑风电不确定性的情况下, 每天运行成本为4 302 052.51元。在不同场景中运营成本和弃风量如表4所示。与场景1相比, 场景2和场景3的运营成本有所增加, 而弃风量的降低是由于减少预测的风力发电量。

表4 在不同场景中的运营成本和弃风量

方案1最终预测运行成本和弃风量分别为4 302 403.35元和167.67 MWh。方案2只考虑DR, 运营成本和弃风量降至4 124 727.04元和137.75 MWh。方案3只考虑HESS, 运营成本为4 296 564.16元, 弃风量为20.66 MWh, 低于方案1和方案2。方案4的结果与方案1、方案2和方案3的结果相比, 同时考虑DR和HESS的电力系统运行更加经济。不同方案中运营成本和弃风量如表5所示。

表5 不同方案中运营成本和弃风量

4 结语

本文综合考虑了风电的不确定性和HESS, 建立了运营成本最低的气电互联综合能源系统日前随机安全调度优化模型, 并将所提出的模型转化为混合整数非线性规划问题。HESS中RSOFC将风能和氢能相互转换, 使用储气罐储存氢。此外, DR被认为是一种基于价格的需求响应机制, 将负荷从高峰时段转移到非高峰时段。考虑DR和HESS的影响, 对系统安全运行进行优化, 研究了综合能源系统的风电消纳和运营成本问题。算例结果表明, 与单独考虑DR或HESS的情况相比, 同时考虑DR和HESS对风电消纳和日常运营成本降低具有积极影响。

参考文献

文献列表

[1]	盛万兴, 吴鸣, 季宇, 等. 分布式可再生能源发电集群并网消纳关键技术及工程实践[J]. 中国电机工程学报, 2019, 39(8): 2175-2186. [本文引用:1]
[2]	方印, 习培玉, 申庆斌, 等. 计及“源-网-荷”成本效益的可再生能源渗透率影响量化分析[J]. 智慧电力, 2019, 47(5): 43-50, 58. [本文引用:1]
[3]	郭鸿业, 陈启鑫, 夏清, 等. 电力市场中的灵活调节服务: 基本概念、均衡模型与研究方向[J]. 中国电机工程学报, 2017, 37(11): 3057-3066, 3361. [本文引用:1]
[4]	史光耀, 邱晓燕, 赵劲帅, 等. 计及风电功率预测误差与需求响应的电力系统滚动调度[J]. 现代电力, 2018, 35(6): 9-15. [本文引用:2]
[5]	苏永新, 聂伟棋, 谭貌. 考虑风电接入和气电转换的综合能源系统日前区间优化[J]. 电力系统自动化, 2019, 43(17): 63-74. [本文引用:1]
[6]	吉兴全, 张广伟, 刘志鹏, 等. 考虑抽水蓄能及电网运营成本的源荷储协调优化调度[J]. 水电能源科学, 2019, 37(3): 191-195. [本文引用:1]
[7]	刘文彬, 柳思岐, 杨子力, 等. 储能对含高风电渗透率系统暂态稳定性的影响[J]. 水电能源科学, 2019, 37(10): 199-203. [本文引用:1]
[8]	唐程辉, 张凡, 张宁, 等. 考虑可再生能源随机性和需求响应的电力系统日前经济调度[J]. 电力系统自动化, 2019, 43(15): 18-25. [本文引用:1]
[9]	施泉生, 丁建勇, 刘坤, 等. 含电、气、热3种储能的微网综合能源系统经济优化运行[J]. 电力自动化设备, 2019, 39(8): 269-276, 293. [本文引用:1]
[10]	徐韵, 颜湘武, 李若瑾, 等. 电力市场环境下含“源-网-荷-储”互动的主动配电网有功/无功联合优化[J]. 电网技术, 2019, 43(10): 3778-3789. [本文引用:1]
[11]	袁桂丽, 董金凤, 魏更, 等. 基于需求响应和多能互补的冷热电联产微网优化调度[J]. 电力建设, 2019, 40(9): 64-72. [本文引用:1]
[12]	袁泉, 吴云亮, 李豹, 等. 计及源荷不确定性的多时间尺度滚动调度计划模型与方法[J]. 电力系统保护与控制, 2019, 47(16): 8-16. [本文引用:1]
[13]	崔杨, 张汇泉, 仲悟之, 等. 计及价格型需求响应及CSP电站参与的风电消纳日前调度[J]. 电网技术, 2020, 40(1): 183-191. [本文引用:1]
[14]	BAI L, LI F, CUI H, et al. Interval optimization based operating strategy for gas-electricity integrated energy systems considering demand response and wind uncertainty[J]. Applied Energy, 2016, 167: 270-279. [本文引用:1]
[15]	汪超群, 韦化, 吴思缘. 计及风电不确定性的随机安全约束机组组合[J]. 电网技术, 2017, 41(5): 1419-1427. [本文引用:1]
[16]	曾丹, 姚建国, 杨胜春, 等. 应对风电消纳中基于安全约束的价格型需求响应优化调度建模[J]. 中国电机工程学报, 2014, 34(31): 5571-5578. [本文引用:1]
[17]	王雅倩, 任娜, 徐宗磊, 等. 电/热/气多能转换的可逆固体氧化物燃料电池信息物理融合建模与仿真[J]. 电网技术, 2018, 42(11): 3535-3542. [本文引用:1]
[18]	王波. 全球最大风电制氢综合利用示范项目整体并网[J]. 能源研究与信息, 2016(32): 163. [本文引用:1]

2019

0.0

... 因此,增加可再生能源的渗透率^[1,2]对电力生产和消费之间的平衡提出了新的挑战 ...

2019

0.0

... 因此,增加可再生能源的渗透率^[1,2]对电力生产和消费之间的平衡提出了新的挑战 ...

2017

0.0

... 为了应对这些挑战,近些年提出了灵活调节服务^[3]、需求响应(Demand Response,DR)与风能的协调^[4,5]、能源存储系统与风电场的协调运行^[6]等方法来解决清洁能源消纳问题 ...

2018

0.0

... 文献[4]研究了DR与风能协调对电力系统运行成本和弃风率的影响 ...

2019

0.0

2019

0.0

2019

0.0

... DR规划在电力系统^[7]和电力市场^[8]可靠经济运行中发挥着重要作用 ...

2019

0.0

... DR规划在电力系统^[7]和电力市场^[8]可靠经济运行中发挥着重要作用 ...

2019

0.0

... 因此,DR可以影响电价,减少高峰负荷,减少弃风,并节约系统运营成本^[9,10] ...

2019

0.0

... 因此,DR可以影响电价,减少高峰负荷,减少弃风,并节约系统运营成本^[9,10] ...

2019

0.0

... 文献[11]提出了基于DR和风、光发电机组与燃气轮机冷热电联产(Combined Cooling,Heating and Power,CCHP)系统结合的优化调度方法,有效降低了系统综合运行成本 ...

2019

0.0

... 文献[12]提出了一种基于偏差预控的负荷调度模式,构建了多时间尺度滚动调度计划模型来实现风电和DR在不同时间尺度上的协调优化 ...

2020

0.0

... 文献[13]在考虑综合成本的前提下,兼顾风电预测和PDR二者的不确定性以及系统安全约束,构建了基于光热电站和PDR参与风电消纳的调度模型 ...

2016

0.0

... 在接入大规模风电的情况下,风电出力的不确定性不可避免地对电力系统安全经济运行造成影响^[14] ...

2017

0.0

... 文献[15]考虑了风电不确定性对电力系统运行调度的影响,提出了基于风电区间预测信息的随机安全约束机组组合模型 ...

2014

0.0

曾丹, 姚建国, 杨胜春, 等. 应对风电消纳中基于安全约束的价格型需求响应优化调度建模[J]. 中国电机工程学报, 2014, 34(31): 5571-5578.

Price-elasticity demand response participates in real-time dispatch to make the accommodation of wind power in a wider geographical region. However, the change of wind power output and load power can cause the branch power flow and node voltage facing the limited risk. It means that security constraints are key factors of the wind power accommodation. Firstly, this paper developed an approach to expound the relationship between the amount of demand response and dispatch economic costs in power grid interaction. Secondly, the static algorithm was described to calculate the amount of interactive response. On the basis of the above content, an optimization dispatch model considering both security constraints and interaction satisfaction of demand response was established. At the same time, it was ensured the objective of minimizing dispatch economic costs and the safety of real-time scheduling operation. Then, we used sensitivity analysis method and interior-point method to solve the model. Finally, we tested the performance of the proposed model by using a case based on a provincial power grid. The results verify that the modeling and solving methods can effectively accommodate the uncertainties of wind power output, and the section transmission power is controlled within the scope of the permit.

China Electric Power Research Institute, Nanjing 210037, Jiangsu Province, China

应对风电消纳问题,价格型需求响应通过价格信号参与电网实时调度,以保持电力供需平衡。然而,风电出力和负荷的改变,使电网潮流和节点电压面临越限风险,从而网络安全约束成为制约风电消纳的关键因素。首先基于价格弹性系数分析价格型需求响应调度成本与互动响应量之间的关系。其次,描述价格型需求响应的互动响应量静态算法,并将其作为预期分配原则之一。在此基础上,同时考虑网络安全约束和价格型需求响应互动响应满意度约束,以电网侧的价格型需求响应调度成本最小化为目标,建立实时优化调度模型,保证实时调度中电网的安全运行。应用灵敏度分析方法将网络安全约束转化为负荷节点互动响应量约束,并通过内点法求解模型。最后,以某省实际电网为例分析验证建模和求解的有效性和可行性,结果表明通过价格型需求响应消纳风电的同时可将稳定断面有功功率控制在允许范围内。

... 文献[16]针对大规模风电并网影响电网稳定运行的问题,提出了最小化风电-抽水蓄能联合系统发电成本模型 ...

2018

0.0

... 在HESS中,由可再生能源产生的过剩功率通过可逆固体氧化物燃料电池(Reversible Solid Oxide Fuel Cell,RSOFC)^[17]中的固体氧化物电解池(Solid Oxide Electrolytic Cell,SOEC)电解转化为氢(Power to Hydrogen,P2H),并存储在储氢罐中 ...

2016

0.0

... 2017年9月8日河北沽源县境内建设的全球最大、国内首个风电制氢综合利用示范项目全部并网发电^[18] ...