基于集合经验模态分解的混合储能系统功率分配

引用本文

郑熙东, 江修波. 基于集合经验模态分解的混合储能系统功率分配[J]. 电器与能效管理技术, 2020(5): 21-27.
ZHENG Xidong, JIANG Xiubo. Power Allocation of Hybrid Energy Storage System Based on Ensemble Empirical Mode Decomposition[J]. ELECTRICAL & ENERGY MANAGEMENT TECHNOLOGY, 2020(5): 21-27.
Doi:10.16628/j.cnki.2095-8188.2020.05.004 复制到剪切板

Permissions

《电器与能效管理技术》编辑部所有

基于集合经验模态分解的混合储能系统功率分配

郑熙东, 江修波

福州大学电气工程与自动化学院, 福建福州 350108

作者简介：

郑熙东(1996—),男,硕士研究生,研究方向为风电并网和储能平抑风电波动。
江修波(1960—),男,教授,研究方向为电力系统运行及管理、电力设备绝缘诊断等。

收稿日期: 2020-01-17

摘要

基于集合经验模态分解(EEMD)对风电波动进行平抑,提出了采用EEMD方法求解出不同的固有模态函数分量和余量。首先,通过信息熵理论求解出固有模态函数能量熵差值最大的阶次作为一个分界点;接着,通过样本熵理论求解出自我相似度最低的阶次作为另一个分界点,通过两个分界点得到初始的功率分配信号;最后,通过模糊控制优化理论对混合储能系统功率分配进行修正。算例分析表明,所提策略能够自适应实现功率合理分配和并网功率平滑,混合储能系统均工作在荷电状态合理区间,能有效提高系统运行稳定性和使用寿命。

关键词: 集合经验模态分解; 能量熵; 样本熵; 模糊控制; 荷电状态

中图分类号:TM731 文献标志码:A 文章编号:2095-8188(2020)05-0021-07 doi: 10.16628/j.cnki.2095-8188.2020.05.004

Power Allocation of Hybrid Energy Storage System Based on Ensemble Empirical Mode Decomposition

ZHENG Xidong¹, JIANG Xiubo²

College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108, China

Abstract

Based on the adaptive ensemble empirical mode decomposition (EEMD),the new method was proposed to reduce the wind power fluctuation.Firstly,the order with the largest difference of the energy entropy of the intrinsic mode function was calculated by the information entropy theory.And then,the order with the lowest self-similarity was calculated by the sample entropy theory.At last,the power distribution of the hybrid energy storage system was modified by the theory of fuzzy control optimization.The results show that the proposed strategy can adaptively realize the reasonable power distribution and grid-connected power smoothing.And the hybrid energy storage system works in the reasonable range of the state of charge,which effectively improves the system stability and service life.

Keyword: ensemble empirical mode decomposition (EEMD); energy entropy; sample entropy; fuzzy control; state of charge

文章图片

0 引言

由于风电的随机性和波动性, 大规模风电并网必然造成系统功率、频率波动, 降低电能质量等, 对风电的大规模并网带来了很大的挑战^[1]。因此, 如何有效运行储能技术进行功率分配, 对风电波动平抑具有重要战略意义^[2]。

风电的波动可以分为高频段和低频段。储能系统参与风电波动平抑, 超级电容可用于高频段小幅的功率波动吸收^[3], 蓄电池则可用于低频段大幅的功率吸收。超级电容作为主要的功率型储能元件, 能够实现频繁的充放电, 具有功率密度大、能量密度小等特点; 蓄电池作为主要的能量型储能元件, 具有功率密度小、能量密度大等特点, 不适合频繁的充放电过程^[4]。

文献[5]采用集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)方法对混合储能系统进行了功率分配, 通过计算储能元件充放电次数, 以系统总成本作为衡量的标准, 对系统进行容量配置优化。文献[6]提出了采用EEMD方法分解多个子序列, 利用广义互信息提取各个子序列的最优输入特征集。文献[7]提出了将EEMD方法用于信号检测与信号特征提取, 能够获得更高的频率分辨率。文献[8]采用EEMD方法求解电弧故障特征层, 经过多类型负载验证, 能够准确识别串联电弧故障。文献[9]通过小波包分解方法得到功率的初次分配, 再通过模糊控制荷电状态优化, 对超级电容和蓄电池进行二次功率分配。文献[10]通过小波包分解出反映并网功率的低频功率波动信号和接入混合储能系统的高频功率信号, 再根据不同储能元件的特点对高频信号再次划分, 最后建立混合储能风电输出平滑模型。文献[11]在混合储能系统中引入功率分配器, 能够动态地调整超级电容和蓄电池的功率分配, 补偿功率之间的不平衡。文献[12]通过EEMD对计算机信号中焦点与非焦点进行分析, 利用单因素方差分析探讨基于熵的特征分离焦点与非焦点计算机信号的能力。

基于上述文献对于EEMD的介绍分析, 没有提及采用能量熵与样本熵对其进行功率分配的方法。本文对风电原始功率波动采用EEMD, 求解出固有模态函数(Intrinsic Mode Function, IMF)分量和余项, 接着采用能量熵对其进行初步的功率分配, 并采用样本熵对其进行补充, 求解出功率分界点k值和J值, 得到初始的功率分配信号。最后通过模糊控制对荷电状态(State of Charge, SOC)优化, 提高混合储能系统的工作效率和使用寿命。

1 风电功率EEMD

EEMD也是一种具有自适应处理输入功率数据的算法, 是在EMD的基础上引入了辅助的噪声数据, 对功率进行高频、低频分解。

1.1 EEMD

在初始信号x₀(t)中添加一个噪声信号f(t), 就能够得到一个新信号X(t):

$X (t) = x_{0} (t) + f (t)$ （1）

类似于小波分解的方法, 采用EMD的分解方法, 逐层分解得到高频、低频IMF分量。

$X (t) = \overset{n}{\sum_{i = 1}} a_{i} (t) + δ (t)$ （2）

式中: a_i(t)— — 分解出来的第i个IMF分量;

δ (t)— — 余项。

不断重复上述公式, 每次重复的过程中加入不同的噪声信号f_j(t), 此时第j次新信号X_j(t)有如下表达:

$X_{j} (t) = \overset{n}{\sum_{i = 1}} a_{ji} (t) + δ_{j} (t)$ （3）

式中: a_ji(t)— — 第j次新信号分解下的第i个IMF分量;

δ _j(t)— — 第j次分解信号的余项。

因此, 最终在总分解次数N次分解之后, 分量和余项有如下表达:

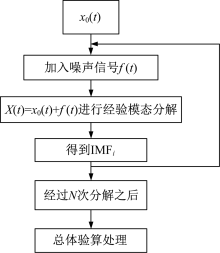
$\{\begin{array}{l} a_{i} (t) = \frac{1}{N} \overset{N}{\sum_{j = 1}} a_{ji} (t) \\ δ (t) = \frac{1}{N} \overset{N}{\sum_{j = 1}} δ_{j} (t) \end{array}$ （4）

因此, EEMD算法步骤如下:

(1) 将一个具有某种函数分布的噪声信号加入到原始的信号中, 构成一个新信号函数。

(2) 将新信号函数进行EMD的原始分解, 得到不同阶次的IMF分量。

(3) 不断重复(1)、(2)步骤, 并且每一次重复都重新加入一个新噪声信号。

(4) 将所得到的IMF分量进行最终处理。

EEMD算法步骤流程图如图1所示。

	Figure Option View Download New Window
	图1 EEMD算法步骤流程图

1.2 信息熵

信息之间是具有相互作用的, 信息本身不可度量, 但是熵的概念是可以度量的, 信息熵则是用来表达信息的一个量化指标。

针对EEMD算法步骤, 对IMF分量的信息熵有如下定义:

$H (IM F_{n}) = - \sum_{i} p (IM F_{n}) \lg p (IM F_{n}), n \in i$ （5）

式中: p(IMF_n)— — IMF_n发生的概率, 特别规定0lg0=0。

然而信息不是单独存在的, 信息与信息之间存在某种关联, 该种关联称之为互信息。互信息是用于衡量两个随机变量之间关联性的度量。在信息论的观点中, 信息之间的关联性越大, 则互信息越多; 反之, 则越少。因此, 引入互信息熵的概念, 两个相邻信息之间的IMF互信息熵有:

$\begin{array}{r} I (IM F_{n}, IM F_{n + 1}) = & H (IM F_{n}) + H (IM F_{n + 1}) - \\ H (IM F_{n} \cdot IM F_{n + 1}) \end{array}$ （6）

式中: I(IMF_n, IMF_n₊₁)— — 相邻两个IMF之间的互信息熵;

H(IMF_n)— — 第n个IMF的信息熵;

H(IMF_n· IMF_n₊₁)— — 联合信息熵。

根据信息理论的相关内容, 假设两个随机变量之间相互独立, 其互信息熵的值为零。因此, 相邻的互信息熵在从高频段到低频段排列的过程中存在一个最小值, 即两个相邻的IMF互信息熵最小。从IMF互信息熵角度入手, IMF信息熵本身是具有能量的, 从能量熵的角度出发, 根据EEMD归一化算法, 能量越大的IMF分量所占权重比越大。基于EMD改进之后的EEMD方法, 归一化的方法能够将所占权重越大的高能量IMF分量突出来, 而所占权重越小的IMF分量则表示能量较低。

因此在分量和余项表达式求解之后, 引入能量熵的概念, 将IMF能量差值最大的定为一个分界点。每一阶的IMF都是具有能量的, 分别为E_i, 总能量为E, 余项也是具有能量的, 在计算式中一般不加入余项的能量^[13]。

$E_{i} = \overset{N}{\sum_{t = 1}} {|a_{i} (t)|}^{2}, i = 1, 2, \dots, n$ （7）

$E = \sqrt[]{\overset{n}{\sum_{i = 1}} E_{i}^{2}}$ （8）

$p_{i} = \frac{E_{i}}{E}, i = 1, 2, \dots, n$ （9）

因此, 相邻两个IMF能量熵的变化越大, 此时能量占比越大, 可以用于区别高频段和低频段, 通过相邻IMF能量熵的变换值作为一个标准阶次k, 将熵值变化最大的阶次作为此时高频、低频对应的标准阶次k。将k之前的高频分量作为超级电容的功率指令, k之后的(包括余项)作为蓄电池的功率指令, 得到初次功率分配指令:

$\{\begin{array}{l} P_{sc} = \overset{k}{\sum_{i = 1}} IM F_{i} \\ P_{bat} = \overset{n - k}{\sum_{i = k}} IM F_{i} + IM F_{δ} \end{array}$ （10）

式中: P_sc— — 超级电容功率指令;

P_bat— — 蓄电池功率指令;

IMF_δ— — IMF的余量;

n— — IMF的总数。

1.3 样本熵

样本熵是和的对数, 能够反映出时间序列复杂性的度量方法。假设有一组已知长度为N的时间序列, 表示为{x(i):1≤ i≤ N}。

首先, 构造一组m维矢量空间向量X(1), X(2), …, X(N-m+1), 其中i=1, 2, …, N-m+1。因此, X(i)为

$X (i) = {x (i), x (i + 1), \dots, x (i + m - 1)}$ （11）

接着, 选取X(i)和X(j)为差值最大的两个向量元素, 定义其最大距离d[X(i), X(j)]为

$d [X (i), X (j)] = \max_{k = 0, 1, \dots, m - 1} |x (i + k) - x (j + k)|$ （12）

对于每个{i, 1≤ i≤ N}, 在容许有偏差为r的前提下, 统计d[X(i), X(j)]< r的数目, 记为N_m₍_i₎, 并将该数目与距离总数目N-m的比值, 记为 $C_{i}^{m}$ (r), 即

$C_{i}^{m} (r) = N_{m} (i) / (N - m)$ （13）

对所有的 $C_{i}^{m}$ (r)求出平均值, 记为C^m(r)。C^m(r)是N-m个 $C_{i}^{m}$ (r)的平均值, 即

$C^{m} (r) = \frac{1}{N - m} \overset{N - m}{\sum_{i = 1}} C_{i}^{m} (r)$ （14）

将维度m增加1, 构成新的m+1维度, 重复上述过程, 得到新的 $C_{i}^{m + 1}$ (r)和C^m⁺¹(r), 即

$C_{i}^{m + 1} (r) = N_{m + 1} (i) / (N - m - 1)$ （15）

$C^{m + 1} (r) = \frac{1}{N - m - 1} \overset{N - m - 1}{\sum_{i = 1}} C_{i}^{m + 1} (r)$ （16）

在理论上, 该序列对应的样本熵为

$SampEn (N, m, r) = \lim_{N \to \infty} [- \ln \frac{C^{m + 1} (r)}{C^{m} (r)}]$ （17）

在实际的求解过程中, N的取值无法达到无穷大, 因此做近似估计:

$SampEn (N, m, r) = - \ln [\frac{C^{m + 1} (r)}{C^{m} (r)}]$ （18）

样本熵的取值和3个参数(N, m, r)有关。重构维数m取值越大, 计算中所需要的数据总数越多。偏差r越小, 则噪声干扰对结果的影响越显著; 偏差r越大, 则信息的损失相应地增大。因此重构维数m一般选择1或2, 优先选择2, 一般不取m> 2; 偏差r一般选择为0.10~0.25。当样本熵的数值越大, 序列的自我相似性越低; 反之, 序列的自我相似性越高。因此, 当样本熵达到最大时, 自我相似性达到最低水平, 因此可以确定为消除噪声的分界值。

在IMF能量熵求解出标准阶次k为初次功率分配指令的基础上, 通过样本熵的原理求解出自我相似性最低的J阶值。将J阶之前的作为超级电容功率指令, J阶之后k阶之前的作为蓄电池功率指令, k阶之后的作为输出功率P_w指令, 得到如下功率分配指令:

$\{\begin{array}{l} P_{sc} = \overset{J}{\sum_{i = 1}} IM F_{i} \\ P_{bat} = \overset{k}{\sum_{i = J}} IM F_{i} \\ P_{w} = \overset{n}{\sum_{i = k}} IM F_{i} + IM F_{δ} \end{array}$ （19）

2 模糊控制优化功率分配

针对充放电条件, 引入SOC的计算约束^[14]:

$SO C_{\min} \leq SO C_{x} \leq SO C_{\max}$ （20）

式中: SOC_max、SOC_min— — 荷电状态的上限和下限。

$SOC (t) = \{\begin{array}{l} (1 - ρ) SOC (t - 1) + \frac{P_{sc} (t) Δ t η_{c}}{E} P (t) > 0 \\ (1 - ρ) SOC (t - 1) - \frac{P_{sc} (t) Δ t}{E η_{d}} P (t) < 0 \end{array}$ （21）

式中: P_sc(t)— — t时刻超级电容功率指令;

SOC(t)、SOC(t-1)— — t时刻和t-1时刻, 经过SOC约束之后超级电容的SOC值;

ρ — — 自放电率;

η _d、η _c— — 放电效率和充电效率;

E— — 超级电容容量。

上述公式主要应对的问题是超级电容在运行的过程中, SOC荷电容量超过上限或者低于下限的情况。当SOC(t)值较低或者较高时, 超级电容P_sc(t)根据不同的充放电情况做出不同的调整。超级电容功率调整方案指令如表1所示。

表1 超级电容功率调整方案指令

因此, 此时的额定容量值E进行如下配置:

$E = \frac{[\max \overset{t}{\sum_{i = 0}} P (t + i) - \min \overset{t}{\sum_{j = 0}} P (t + j)] Δ t}{SO C_{\max} - SO C_{\min}}$ （22）

式中:P(t+i)、P(t+j)— — 储能t+i时刻和t+j时刻的功率;

Δ t— — 相应的时间间隔, t=NΔ t;

N— — 总时间段的个数。

模糊控制器的输入包括两部分, 为t-1时间段结束后功率型储能元件荷电状态SOC(t-1)和t时间段结束后功率型储能元件荷电状态的变化Δ SOC(t); 输出为功率型储能元件功率调节系数K_p。模糊控制输入、输出与隶属度函数曲线如图2所示。

	Figure Option View Download New Window
	图2 模糊控制输入、输出与隶属度函数曲线

SOC模糊控制优化的根本思想是减少能量型储能元件的过度使用, 减少系统对能量型储能元件的损害影响; 在充分发挥功率型储能元件使用特性的过程中, 当SOC接近上、下限值时, 将部分功率分配至能量型储能元件, 进行二次功率分配。模糊控制规则如表2所示。

表2 模糊控制规则

在模糊控制SOC优化后, 得到新的超级电容和蓄电池的功率分配指令:

$\{\begin{array}{l} P'_{sc} = K_{p} P_{sc} \\ P'_{bat} = P_{bat} + (1 - K_{p}) P_{sc} \end{array}$ （23）

式中: P'_sc— — 新超级电容功率分配指令;

P'_bat— — 新蓄电池功率分配指令。

3 算例分析

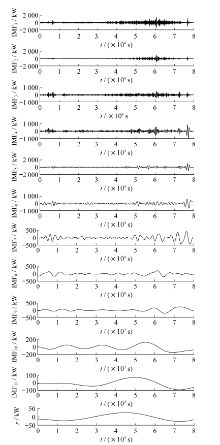
根据EEMD得到11个阶次对应的IMF分量和余量的波动曲线。IMF各阶次分量与余量如图3所示。

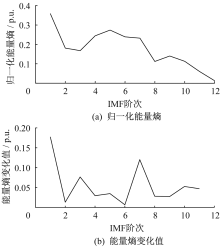
	Figure Option View Download New Window
	图3 IMF各阶次分量与余量

不同阶次的IMF分量和余量都是具有能量的, 通过归一化的算法, 能量越大的IMF分量所占的权重比也越大。因此, IMF各阶归一化能量熵与变化值如图4所示。

	Figure Option View Download New Window
	图4 IMF各阶归一化能量熵与变化值

通常根据风电功率低频段和中高频段的区分, IMF能量占比权重高低通过归一化的方法p_i求解出。因此, 根据IMF能量熵变换滤波的阶次k, 确定风电功率低频、中高频的区分。一般归一化的过程中, 容易出现IMF变换值首末端最大的情况, 如果根据能量熵差值最大的点来分配, 容易出现蓄电池和超级电容分配失误的情况。根据上述IMF能量熵变换值可以看到, 在IMF第7阶和第8阶之间, 存在一个除首末端的最大变化值, 因此选择k=8作为分界。超级电容和蓄电池的功率指令为

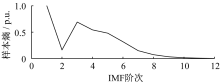
$\{\begin{array}{l} P_{sc} = \overset{7}{\sum_{i = 1}} p_{i} \\ P_{bat} = \overset{11}{\sum_{i = 8}} p_{i} + p_{δ} \end{array}$ （24）

接着求解出不同IMF阶次对应的样本熵值, IMF阶次对应样本熵如图5所示。

	Figure Option View Download New Window
	图5 IMF阶次对应样本熵

由图5可见, IMF₁存在最大的样本熵。当样本熵值达到最大时, 自我相似性达到最低水平。如果J=1, 无法让蓄电池处于最佳的工作状态, 也无法发挥超级电容的特性, 因此选择J=3, 确定为消除噪声的分界值。

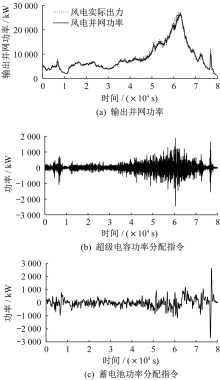
$\{\begin{array}{l} P_{sc} = \overset{3}{\sum_{i = 1}} IM F_{i} \\ P_{bat} = \overset{7}{\sum_{i = 4}} IM F_{i} \\ P_{w} = \overset{11}{\sum_{i = 8}} IM F_{i} + IM F_{δ} \end{array}$ （25）

本文采用30 MW风电场原始数据, 根据上述公式求解出原始数据和并网输出功率曲线, 以及超级电容与蓄电池的功率分配指令。输出并网功率和超级电容、蓄电池功率分配指令如图6所示。

	Figure Option View Download New Window
	图6 输出并网功率和超级电容、蓄电池功率分配指令

由图6可见, 根据EEMD方法获得的并网功率具有很好的风电输出跟踪滤波作用, 能够得到比较平滑的输出功率。超级电容和蓄电池的功率分配中, 超级电容承担更多高频段的功率波动, 蓄电池承担更多低频段的功率波动, 并且充放电次数相对较少, 提高了蓄电池的使用寿命。

混合储能系统参数配置如表3所示。

表3 混合储能系统参数配置

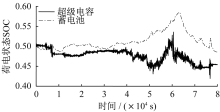
根据模糊控制的参数配置, 得到模糊控制优化后超级电容和蓄电池SOC曲线, 如图7所示。

	Figure Option View Download New Window
	图7 模糊控制优化后超级电容和蓄电池SOC曲线

由图7可见, 蓄电池SOC为0.45~0.60, 超级电容SOC为0.40~0.55。超级电容在工作过程中SOC基本在0.5浮动, 当超级电容SOC相对较低时, 减少对超级电容继续执行放电指令; 同理当超级电容SOC相对较高时, 减少对其继续执行充电指令, 使其保持在相对稳定的状态。对于蓄电池而言, 整体并无较大的变化, 而是继续维持相对平滑稳定, 减少蓄电池频繁充放电过程, 提高了整体混合储能系统的使用效率^{[15, 16]}。

4 结语

本文采用了EEMD求解出不同阶次对应的IMF分量和余量, 求解出IMF对应的能量熵, 确定分界点k, 再求出样本熵对应的J, 得到新的功率能量分配。通过模糊控制和SOC优化的方法, 最终求解出优化后的超级电容和蓄电池的功率曲线。仿真结果表明, 通过能量熵和样本熵确定的能量分配方法, 结合模糊控制理论能够有效平抑风电波动, 使不同储能元件处于合理的SOC区间, 并能够得到平滑的并网功率曲线。本文是在EEMD的基础上研究的, 后续将针对EEMD方法, 设计“ N+1” 储能系统(N个混合储能系统和1个备用系统)进行优化分析, 并结合小波包分解的方法。

参考文献

文献列表

[1]	崔炜, 艾斯卡尔. 国内外风电技术现状与发展趋势[J]. 电器与能效管理技术, 2019(13): 1-5. [本文引用:1]
[2]	韩志坚, 吴光敏, 张文斌, 等. 混合储能在变电站直流系统中的功率分配[J]. 电器与能效管理技术, 2015(22): 64-67, 72. [本文引用:1]
[3]	刘卫健, 黎淑娟, 黄际元, 等. 储能参与风电并网系统的波动平抑控制研究[J]. 电器与能效管理技术, 2018(16): 41-47, 66. [本文引用:1]
[4]	ZHAO P, WANG J F, DAI Y P. Capacity allocation of a hybrid energy storage system for power system peak shaving at high wind power penetration level[J]. Renewable Energy, 2015, 75: 541-549. [本文引用:1]
[5]	孙威, 房凯, 李颖, 等. 基于EEMD的微电网混合储能系统规划方法[J]. 电器与能效管理技术, 2018(1): 66-74. [本文引用:1]
[6]	LI C, KONG X, WANG X, et al. Short-term wind power forecasting method based on mode decomposition and feature extraction[C]∥2019 22nd International Conference on Electrical Machines and Systems (ICEMS), 2019: 1-5. [本文引用:1]
[7]	YANG L, ZHANG L. Research on signal detection based on EEMD and energy entropy[C]∥2016 IEEE/OES China Ocean Acoustics (COA), 2016: 1-4. [本文引用:1]
[8]	张冠英, 曹旺林, 李长伟, 等. 基于集合经验模态分解的串联型故障电弧辨识方法[J]. 电器与能效管理技术, 2016(5): 8-12. [本文引用:1]
[9]	吴杰, 丁明. 采用自适应小波包分解的混合储能平抑风电波动控制策略[J]. 电力系统自动化, 2017, 41(3): 7-12. [本文引用:1]
[10]	韩晓娟, 陈跃燕, 张浩, 等. 基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J]. 中国电机工程学报, 2013, 33(19): 8-13, 24. [本文引用:1]
[11]	FENG X, GOOI H B, CHEN S X. Hybrid energy storage with multimode fuzzy power allocator for PV systems[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 389-397. [本文引用:1]
[12]	DAS A B, BHUIYAN M I H. Discrimination of focal and non-focal EEG signals using entropy-based features in EEMD and CEEMDAN domains[C]∥2016 9th International Conference on Electrical and Computer Engineering (ICECE), 2016: 435-438. [本文引用:1]
[13]	谢超, 张建文, 李星. 基于EMD与模糊控制的混合储能控制策略[J]. 电测与仪表, 2019, 56(20): 124-129. [本文引用:1]
[14]	吴振威, 蒋小平, 马会萌, 等. 用于混合储能平抑光伏波动的小波包-模糊控制[J]. 中国电机工程学报, 2014, 34(3): 317-324. [本文引用:1]
[15]	王洪, 卢志涛, 王少博, 等. 基于人工智能的电网用蓄电池健康度评估[J]. 广东电力, 2019, 32(4): 79-84. [本文引用:1]
[16]	杨清波, 汪娟娟, 黄骏翅, 等. 基于多因素的储能系统剩余电量估计方法[J]. 广东电力, 2018, 31(2): 32-37. [本文引用:1]

2019

0.0

... 0 引言由于风电的随机性和波动性,大规模风电并网必然造成系统功率、频率波动,降低电能质量等,对风电的大规模并网带来了很大的挑战^[1] ...

2015

0.0

... 因此,如何有效运行储能技术进行功率分配,对风电波动平抑具有重要战略意义^[2] ...

2018

0.0

... 储能系统参与风电波动平抑,超级电容可用于高频段小幅的功率波动吸收^[3],蓄电池则可用于低频段大幅的功率吸收 ...

2015

0.0

... 蓄电池作为主要的能量型储能元件,具有功率密度小、能量密度大等特点,不适合频繁的充放电过程^[4] ...

2018

0.0

... 文献[5]采用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法对混合储能系统进行了功率分配,通过计算储能元件充放电次数,以系统总成本作为衡量的标准,对系统进行容量配置优化 ...

2019

0.0

... 文献[6]提出了采用EEMD方法分解多个子序列,利用广义互信息提取各个子序列的最优输入特征集 ...

2016

0.0

... 文献[7]提出了将EEMD方法用于信号检测与信号特征提取,能够获得更高的频率分辨率 ...

2016

0.0

... 文献[8]采用EEMD方法求解电弧故障特征层,经过多类型负载验证,能够准确识别串联电弧故障 ...

2017

0.0

... 文献[9]通过小波包分解方法得到功率的初次分配,再通过模糊控制荷电状态优化,对超级电容和蓄电池进行二次功率分配 ...

2013

0.0

韩晓娟, 陈跃燕, 张浩, 等. 基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J]. 中国电机工程学报, 2013, 33(19): 8-13, 24.

On base of the full analysis for the amplitude frequency characteristics of wind power, a hybrid energy storage system (HESS) based on wavelet packet decomposition in smoothing the fluctuations of wind power is proposed in this paper. The power output signals at a wind farm were decomposed into low frequency signals as grid-connected power and high frequency signals connected into energy storage system by wavelet packet decomposition theory. According to the characteristics of different types of energy storage system, the high frequency signals are divided into different frequency ranges adapting to the batteries and the super capacitors respectively so that the smoothing control model of wind power based on hybrid energy storage system is established. Compared with the smoothing result obtained by the batteries, the simulation examples show that the method provided in this paper can effectively restrain the fluctuations of wind power and improve the use life of the batteries, which has a certain engineering application prospect.

School of Control and Computer Engineering, North China Electric Power University, Changping District, Beijing 102206, China

在充分分析风电功率幅频特性的基础上，提出基于小波包分解的混合储能技术平抑风电场输出功率波动的方法。采用小波包分解理论对风电场输出功率信号进行多尺度分解，得到反映并网功率信号的低频信号和接入储能系统的高频信号；根据不同类型储能系统的特点，将高频信号再次进行划分，分别选择与其频率范围适应的电池和超级电容器储能设备，建立了基于混合储能系统的风电场输出功率平滑控制模型；与单类型电池储能系统功率平滑效果进行了对比。仿真实例表明：该方法能够有效地抑制风电场输出功率的波动，提高储能电池的使用寿命，具有一定的工程应用价值。

... 文献[10]通过小波包分解出反映并网功率的低频功率波动信号和接入混合储能系统的高频功率信号,再根据不同储能元件的特点对高频信号再次划分,最后建立混合储能风电输出平滑模型 ...

2014

0.0

... 文献[11]在混合储能系统中引入功率分配器,能够动态地调整超级电容和蓄电池的功率分配,补偿功率之间的不平衡 ...

2016

0.0

... 文献[12]通过EEMD对计算机信号中焦点与非焦点进行分析,利用单因素方差分析探讨基于熵的特征分离焦点与非焦点计算机信号的能力 ...

2019

0.0

... 每一阶的IMF都是具有能量的,分别为E_i,总能量为E,余项也是具有能量的,在计算式中一般不加入余项的能量^[13] ...

2014

0.0

吴振威, 蒋小平, 马会萌, 等. 用于混合储能平抑光伏波动的小波包-模糊控制[J]. 中国电机工程学报, 2014, 34(3): 317-324.

In this paper, a hybrid energy storage system consisting of energy-type storage system and power-type storage system is used to smooth the PV power generation fluctuations. With a comprehensive analysis of the amplitude-frequency characteristics of PV power signal and the performances characteristics of different energy storage systems, the PV power signal is decomposed and the smoothing objective power and the charging and discharging power of energy storage systems are obtained by wavelet packet decomposition which can get more signals’ detail information. Full consideration is given to the real-time control requirements for computing speed in practical application, and the filter delay effect is compensated through threshold judgment. SOC adaptive control of power-type storage system using fuzzy control method is applied to achieve optimal allocation and improve smoothing result. Numerical results show that the proposed control strategy can smooth the PV power generation fluctuations effectively by taking full advantages of the performance benefits of different types of energy storage systems.

1. School of Mechanical Electronic & Information Engineering, China University of Mining & Technology, Haidian District, Beijing 100083, China; 2.China Electrical Power Research Institute, Haidian District, Beijing 100192, China

采用能量型储能和功率型储能组成的混合储能系统平抑光伏输出功率波动。利用小波包分解可获取更多信号细节信息的优点, 综合分析光伏功率信号的幅频特性、储能的性能特点, 将光伏功率信号分解, 得到光伏平抑目标功率和不同类型储能的充放电功率。充分考虑实际工程应用中实时控制对运算速度的要求, 并通过阈值判断补偿滤波延迟效应。采用模糊控制方法对功率型储能的荷电状态(state of charge, SOC)进行自适应控制, 实现功率的优化分配, 提高平抑效果。算例结果表明, 所提控制策略能够充分利用不同类型储能的性能优势有效平抑光伏输出功率波动。

... 2 模糊控制优化功率分配针对充放电条件,引入SOC的计算约束^[14]: ...

2019

0.0

... 对于蓄电池而言,整体并无较大的变化,而是继续维持相对平滑稳定,减少蓄电池频繁充放电过程,提高了整体混合储能系统的使用效率^[15,16] ...

2018

0.0

... 对于蓄电池而言,整体并无较大的变化,而是继续维持相对平滑稳定,减少蓄电池频繁充放电过程,提高了整体混合储能系统的使用效率^[15,16] ...