无线电能传输(Wireless Power Transfer, WPT)技术作为一种新型电能传输方式, 一直是各国学者的研究热点, 在许多场合展现出了良好的应用前景, 如便携式电器、汽车、医疗人体植入器件、矿井开发等。最早提出无线电能传输设想的是尼古拉· 特斯拉, 但由于各种原因, 其发展停滞不前。2007年, 麻省理工学院的研究团队提出磁耦合谐振式WPT技术^[1], 这一研究成果使得该技术飞速发展, 各国学者对此进行了深入的研究^{[2, 3]}。目前, 效率与距离的矛盾仍然是限制WPT技术广泛应用的一大难题, 随着传输距离增加、耦合系数减小, 系统效率将急剧下降。

2017年, Assawaworrarit团队利用宇称时间(Parity-Time, PT)对称原理, 在WPT系统中引入非线性饱和增益机制, 使得耦合线圈在1 m距离内能实现恒定高效电力传输^[4]。文献[5]将非线性PT对称应用于给引信供电的系统中, 采用电路分析方法, 再次验证了该理论的有效性。文献[6]从耦合模理论和电路理论两方面出发, 分析了非线性PT对称系统通过改变工作频率使其效率维持恒定的原理。但这些已有的系统采用运算放大器引入反馈来提供饱和增益, 导致系统传输功率小。为解决这一问题, 本文使用电力开关器件作为非线性饱和增益元件来实现PT对称系统, 并分析了其工作原理, 为PT对称理论在WPT中的进一步应用提供了参考。

本文采用耦合模理论揭示非线性PT对称WPT系统的原理。根据文献[1]给出耦合模公式:

dαmdt=(jωm-γm)αm+∑jkmnαn(t)+Fm(1)

式中: |α _m|²— — 谐振体包含的能量;

ω _m— — 谐振体固有角频率;

k_mn— — 谐振体之间的耦合系数;

γ _m— — 谐振体衰减系数;

F_m— — 给予谐振体的激励。

基于运算放大器的PT对称WPT系统如图1所示。其中L₁、L₂分别为发射线圈和接收线圈的自感; K为两线圈的耦合系数; C₁、C₂分别为两线圈匹配谐振电容。

图1

	Figure Option ViewDownloadNew Window
	图1 基于运算放大器的PT对称WPT系统

假定|α ₁|²、|α ₂|²分别为发射线圈和接收线圈包含的能量; ω ₁、ω ₂分别为两线圈的固有谐振频率; k为两线圈的耦合系数, 且k=k₁₂=k₂₁。系统耦合模公式如下:

dα1dt=(jω1+g1)α1-jkα2dα2dt=(jω2-γ2)α2-jkα1(2)

其中, g₁=g₁₀-γ ₁₀, γ ₂=γ ₂₀+γ ₂₁。

式中: g₁— — 发射端总增益率;

g₁₀— — 增益电路的增益率;

γ ₁₀— — 发射线圈的损耗率。

γ ₂— — 接收端的损耗率;

γ ₂₀— — 接收线圈的损耗率;

γ ₂₁— — 负载的损耗率。

为了得到稳态状态下系统的解, 根据文献[7]可知, α ₁、α ₂与e^jwt成正比, 由此可得特征方程如下:

[j(ω1-ω)+g1][j(ω2-ω)-γ2]+k2=0(3)

当耦合系数增益k发生变化时, 增益g₁会随之变化, 要得到方程实数解。定义饱和增益g_s:

gs=γ2ω-ω1ω-ω2(4)

分离式(3)的实部和虚部可以得到:

(ω-ω1)(ω-ω2)2+γ22(ω-ω1)-k2(ω-ω2)=0(5)

假设系统频率与两线圈自谐振频率相等, ω ₀=ω ₁=ω ₂, 由式(4)和式(5)得:

ω=ω0±k2-γ2, gs=γ2ω0, gs=k2γ2(6)

由式(6)可知, 系统谐振频率会随耦合系数k的变化作相应调整, 维持增益系统和损耗系统的平衡, 这就是PT对称电路的饱和增益机制。当系统位于强耦合区间(k≥ γ ₂)时, 式(3)有两个实数解, 此时系统有两个谐振频率; 当系统位于弱耦合区间(k< γ ₂)时, 方程只有一个实数解, 此时系统只有一个谐振频率。由于耦合系数k恒小于1, 因此饱和增益g_s=k²/γ ₂恒小于系统接收端衰减率, 饱和增益无法补偿系统损耗。根据文献[7]的耦合模理论分析可以得到WPT的效率η 公式:

η=2γ21|α2|22γ10|α1|2+2γ2|α2|2=γ21γ2+γ10γ22k2, k< γ2γ21γ2+γ10γ2γ2, k≥γ2(7)

根据式(7), 当系统处于强耦合区间(k≥ γ ₂)时, 效率与耦合系数k无关。由于发射线圈的损耗率γ ₁₀远小于接收端损耗率γ ₂, 接收线圈的损耗率γ ₂₀远小于负载的损耗率, 此时效率为

η=γ21γ2+γ10γ2γ2≈1(8)

即在强耦合区, 系统可以通过增益电路自动补偿负载损耗达到效率恒定不变的目的。

当系统处于弱耦合区间(k< γ ₂)时, 由式(7)可知, 系统效率随耦合系数k的减小而降低。

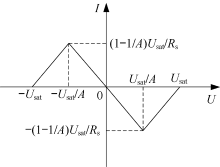
基于运放非线性增益电路U-I特性如图2所示。由图2可见, 由于运算放大器的非线性饱和特性, 电压、电流特性呈现出分段的形式, 在不同时刻, 增益电路起到不同的作用。根据文献[8]给出的分析, 起始时刻, 发射线圈中的能量|α ₁|²很小, 增益电路相当于负电阻-R_s/(A-1)往发射线圈输送能量, 电阻值R_s/(A-1)小于负载电阻R_l, |α ₁|²呈指数增长到一定值, 随后增益电路又相当正电阻R_s, |α ₁|²呈指数减少, 增益电路又作为负电阻起到供能作用, 如此循环, 最终增益负电阻与损耗负载电阻大小相同, 增益与损耗达到一致, 系统稳定工作。

图2

	Figure Option ViewDownloadNew Window
	图2 基于运放非线性增益电路U-I特性

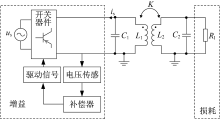
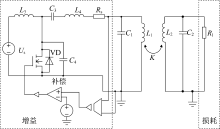
基于开关器件的PT对称WPT系统如图3所示。通过搭建反馈回路实时监测谐振电路的工作情况, 利用电压传感器和比较器将调节信息传递给驱动电路, 控制开关电路的输出。基于开关器件的PT对称WPT系统如图3所示。

图3

	Figure Option ViewDownloadNew Window
	图3 基于开关器件的PT对称WPT系统

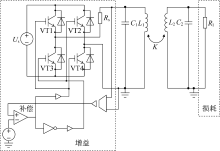
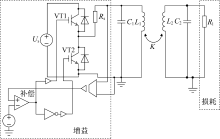
基于以上理论分析, 采用电力电子仿真软件PSIM对图3中的原理图进行建模仿真。基于全桥、半桥电路和E类功率放大器的PT对称WPT系统分别如图4~图6所示。传输部分固有谐振频率为6.78 MHz, 具体系统参数如表1所示。通过开关电路和电阻R_s组成增益系统, 负载R_l作为损耗系统, 忽略开关延迟对开关器件的影响, 电压传感器将谐振回路电压传递给比较器, 当谐振回路电压为正时, 开关电路同样输出正电压, 反之亦然。开关电路的输出电压受到直流电压源U_s的限制, 为系统提供饱和增益。当发射线圈的能量|α ₁|²很小时, 开关电路通过电阻R_s向发射线圈供能, 在强耦合区, 随着耦合系数的改变, 系统工作频率会发生变化, 通过改变增益来维持恒定的效率。

图4

	Figure Option ViewDownloadNew Window
	图4 基于全桥电路的PT对称WPT系统

图5

	Figure Option ViewDownloadNew Window
	图5 基于半桥电路的PT对称WPT系统

图6

	Figure Option ViewDownloadNew Window
	图6 基于E类功率放大器的PT对称WPT系统

表1

表1

表1 具体系统参数 参数 数值 参数 数值 Us/V 20 K 0~0.2 Rs/Ω 10 C3/pF 120 C1, 2/nF 100 L3/μ H 35 L1, 2/nH 5.51 C4/pF 270 R1/Ω 70 L4/μ H 20

表1 具体系统参数

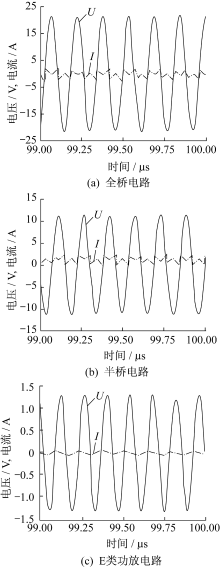
耦合系数为0.1时, 非线性增益电路输出波形如图7所示。

图7

	Figure Option ViewDownloadNew Window
	图7 非线性增益电路输出波形

由图7可见, 当系统稳定运行时, 增益部分的输出电压和电流是同相位的, 由于线圈与电容为并联连接, 其品质因数很高, 输出电压为稳定的正弦波。而输出电流是非线性波, 被一饱和值所约束, 体现增益电路的非线性负电阻特性, 符合分析结果。

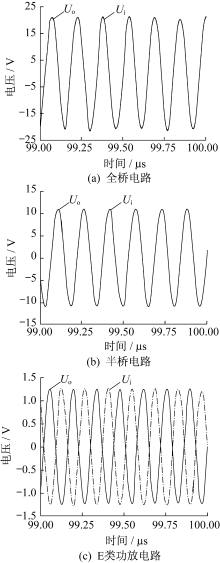
耦合系数为0.1时, 系统传输部分电压波形如图8所示。

图8

	Figure Option ViewDownloadNew Window
	图8 系统传输部分电压波形

由图8可见, 接收线圈两端电压U₀与发射线圈两端电压U_i的幅值几乎相等。根据文献[5]可知, 由于PT系统的对称性, 系统的传输效率可表示为

η=|U0|2|Ui|2=U0I0UiIi(9)

因此, 系统的传输效率接近100%, 与分析一致。

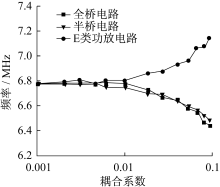
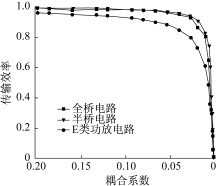
通过测量电压波形的周期, 可以得到系统的谐振频率。通过记录在不同耦合系数下传输系统谐振时U₀和U_i的幅值和周期, 系统谐振频率和传输效率随耦合系数k的变化分别如图9和图10所示。

图9

	Figure Option ViewDownloadNew Window
	图9 系统谐振频率随耦合系数的变化关系

图10

	Figure Option ViewDownloadNew Window
	图10 系统传输效率随耦合系数的变化关系

根据分析可知, 系统在强耦合区(k≥ γ ₂), 支持两种实数模式, 谐振频率为ω =ω ₀± k2-γ2, 即系统拥有两个频率分支。由图9可知, 由全桥和半桥作为非线性饱和增益的PT对称WPT系统, 在强耦合区, 系统工作频率优先选择了低频分支。而由E类功放作为非线性饱和增益的PT对称WPT系统, 在强耦合区, 系统工作频率优先选择高频分支。

由图10可见, 在耦合系数k≥ 0.025时, 三种类型的PT对称WPT系统均能维持较高传输效率, 在耦合系数k< 0.025时, 系统传输效率迅速衰减。在实际情况中, 系统耦合系数和传输距离呈一定的对应关系, 这表明采用全桥、半桥、E类功放的PT对称WPT系统在一定距离内可以维持恒定高效的传输。

本文介绍了PT对称WPT系统的原理, 通过耦合模理论分析了其维持恒定高效传输的机理, 提出了一种基于开关器件的非线性PT对称WPT系统, 通过仿真验证了理论的正确性。结论如下:

(1)采用全桥、半桥、E类功放电路作为非线性饱和增益电路的WPT系统可以实现PT对称的特性。

(2)系统谐振线圈在强耦合区(k≥ γ ₂)内, WPT系统能维持稳定高效的传输, 超出强耦合区范围(k< γ ₂), 系统效率将会迅速衰减。