一种塑壳断路器操作机构及受力分析研究

引用本文

唐庭, 汪泰宇, 徐朋生, 谢凌峰. 一种塑壳断路器操作机构及受力分析研究[J]. 电器与能效管理技术, 2020(4): 47-53.
TANG Ting, WANG Taiyu, XU Pengsheng, XIE Lingfeng. Study on Operation Mechanism and Stress Analysis of MCCB[J]. ELECTRICAL & ENERGY MANAGEMENT TECHNOLOGY, 2020(4): 47-53.
Doi:10.16628/j.cnki.2095-8188.2020.04.009 复制到剪切板

Permissions

《电器与能效管理技术》编辑部所有

一种塑壳断路器操作机构及受力分析研究

唐庭, 汪泰宇, 徐朋生, 谢凌峰

环宇集团浙江高科股份有限公司,浙江温州 325603

作者简介：

唐庭(1987—),男,工程师,主要从事断路器的研究和应用。
汪泰宇(1964—),男,教授级高级工程师,主要从事塑壳断路器的研究和应用。
徐朋生(1987—),男,工程师,主要从事断路器的开发。

收稿日期: 2019-12-27

摘要

根据塑壳断路器(MCCB)操作机构的连杆转化特点及静态特性,绘制了各个关键状态的机构简图,并详细阐述了操作机构的运动原理;同时采用图解法对操作机构的各杆件在某些稳定状态位置及特定瞬态位置进行受力分析,并利用力学平衡原理及正弦定理计算出MCCB的关键五大力学参数:手柄再扣力、手柄合闸力、主拉簧力、触头终压力、脱扣力,为现有的MCCB的操作机构的受力优化及全新的操作机构的设计提供了理论参考。

关键词: 塑壳断路器; 操作机构; 受力分析; 图解法; 力学平衡; 正弦定理

中图分类号:TM561 文献标志码:A 文章编号:2095-8188(2020)04-0047-07 doi: 10.16628/j.cnki.2095-8188.2020.04.009

Study on Operation Mechanism and Stress Analysis of MCCB

TANG Ting, WANG Taiyu, XU Pengsheng, XIE Lingfeng

Zhejiang High Tech Co.,Ltd.,Huanyu Group,Wenzhou 325603,China

Abstract

According to the connecting rod transformation characteristics and static characteristics of the moulded case circuit breaker(MCCB) operation mechanism,the mechanism sketches of each key state were drawn,and the movement principle of the operation mechanism was elaborated in detail.On the other hand,the force analysis of the links of the operation mechanism in some stable and specific transient positions was carried out by graphic method,and the key mechanical parameters of MCCB were calculated by using the principle of mechanical balance and the theorem of positive rotation.These five mechanical parameters are the re-buckling force of the handle,the closing force of the handle,the main spring force,the final contact pressure and the release force.It provides a theoretical reference was provided for the force optimization of the existing MCCB operating mechanism and the design of a new operating mechanism.

Keyword: moulded case circuit breaker(MCCB); operating mechanism; force analysis; graphic method; mechanical balance; positive rotation theorem

文章图片

0 引言

塑壳断路器(Moulded Case Circuit Breaker, MCCB)广泛应用于工业配电系统中, 处于整个电网的中间部分, 上级连接着万能式断路器, 下级连接着小型断路器, 起着纽带的作用。MCCB主要部件包括操作机构、触头系统、灭弧系统等, 操作机构作为MCCB的执行机构, 更是MCCB整个系统的核心机构^[1]。操作机构的优劣直接影响断路器的可靠性、稳定性, 因此MCCB的操作机构性能得到了很大的关注与研究。不少专家都对MCCB的操作机构性能开展了各个方面的研究。周宏明等^[2]通过采用拉格朗日方程建立了断路器操作机构的动力学模型, 分析了操作机构的等效转动惯量和广义作用力; 陈德桂等^[3]通过建立简化的三维模型, 对操作机构的弹簧刚度、分断时间和分断速度进行了深入分析; 蒋顾平等^[4]通过三维建模仿真, 分析了操作机构的关键轴位置、杆件质量、连杆转化位置对操作机构动作速度的影响; 苏秀萍等^[5]采用有限元分析法对MCCB连杆机构的可靠性进行了分析。

以上这些研究分析都为MCCB的操作机构特性提供了有价值的论证, 但侧重点各不相同。有的阐述了操作机构的设计方法, 有的分析了操作机构的分断速度及时间, 有的研究了操作机构的可靠性等, 而本文则着重从力学的角度, 通过对MCCB操作机构运动简图的绘制, 运用最直观的图解法对操作机构进行受力分析, 并利用力学平衡原理及正弦定理计算出MCCB的关键五大力学参数。这对现有MCCB操作机构的受力分析有更加深入的理解, 有助于解决生产过程中产品机构的滑扣、死扣、脱扣力偏大等问题, 同时对全新机构的设计研究具有重要的参考意义。

1 MCCB操作机构动作原理分析

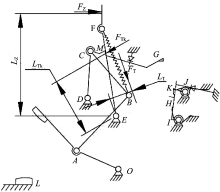
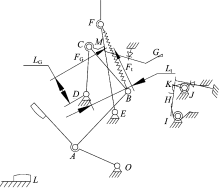
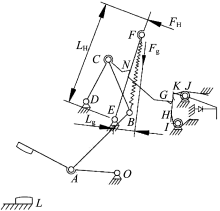
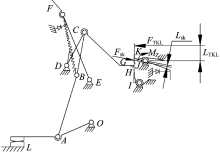
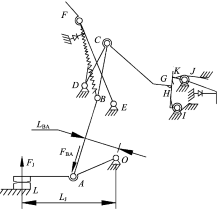
本文选取HUM8-250产品作为研究对象, 对操作机构运动原理进行分析, 画出各个机构件的受力示意图, 利用操作机构稳定状态的力学平衡原理及操作机构瞬时时刻的受力分解, 正弦定理计算出MCCB的手柄再扣力、手柄合闸力、主拉簧力、触头终压力、脱扣力。MCCB操作机构模型如图1所示。

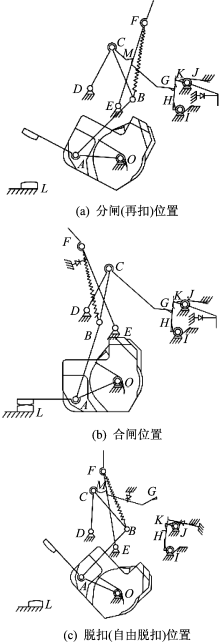
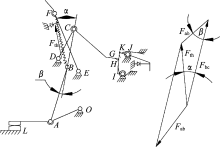
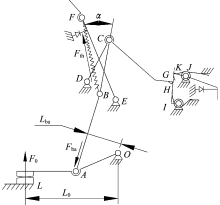
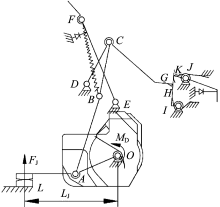
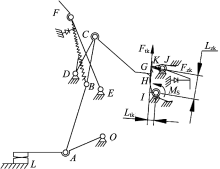
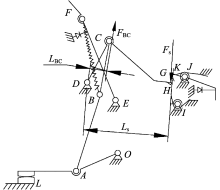
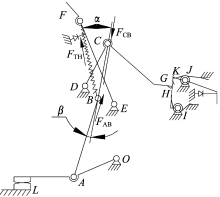
	Figure Option View Download New Window
	图1 MCCB操作机构模型

MCCB 3种位置的操作机构简图如图2所示。其中, OA为动触头, AB为下连杆, BC为上连杆, DCG为跳扣杆, EF为杠杆, IH为锁扣, JK为再扣杆, BF为连接轴B和杠杆间的主拉簧, L为静触头, M为脱扣状态时杠杆和跳扣的接触点, N为再扣时杠杆和跳扣的接触点, ODEIJ为基座, 同时触头、跳扣、锁扣上都装有各自的反力扭簧。

	Figure Option View Download New Window
	图2 MCCB 3种位置的操作机构简图

断路器虽然不断地更新换代, 但是操作机构万变不离其宗, 都是四连杆或五连杆机构。断路器在分闸(再扣)或合闸时, 锁扣IH被再扣杆JK的K点锁住, 同时带动跳扣杆DCG的G点被锁扣IH的H点锁住, 这样C点相对于机架静止不动, 此时OA、AB、BC、OC组成了四连杆机构。四连杆机构具有一个自由度, 只要其中的一个连杆位置确定后, 其他位置连杆也会相应确定, 故操作机构能实现一种动作, 即手柄带动触头分闸或合闸动作。断路器在自由脱扣时, 再扣杆JK的K点对锁扣IH的限制作用消失, 同时带动锁扣IH的H点对跳扣杆DCG的G点限制作用消失, 锁扣IH的H点与跳扣杆DCG的G点分离, 增加了机构的自由度, 此时OA、AB、BC、CD、OD组成了五连杆机构。五连杆机构具有两个自由度, 故操作机构能实现绕D点向前、向后运动。

断路器脱扣过程:当电路过载或短路时, 牵引杆在双金属片形变力或电磁力的作用下(此力大于机构脱扣力), 带动再扣杆JK绕J点逆时针转动, 此时再扣杆JK的K点对锁扣IH的限制作用消失, 锁扣IH绕I点顺时针转动, 锁扣IH的H点对跳扣杆DCG的G点限制作用也消失, 在主拉簧弹簧力的作用下, 连杆BC钩着跳扣杆DCG的C点, 一起绕D点逆时针转动, 并带动连杆AB、动触头OA一起绕O点顺时针转动, 从而实现分断。

断路器分闸(再扣)过程:由于锁扣IH被再扣杆JK的K点锁住, 带动跳扣杆DCG的G点被锁扣IH的H点锁住, 此时杠杆EF在外力(分闸力)的作用下绕E点顺时针转动, 直到F点由上连杆BC连线的左边运动到BC连线的右边, 主拉簧的弹簧力将使连杆BC绕C点逆时针转动并带动下连杆AB、动触头OA一起绕O点顺时针转动, 从而实现动、静触头分离。

断路器合闸过程:与分闸过程一样, 跳扣杆DCG的G点被锁扣IH的H点锁住, 此时杠杆EF在外力(合闸力)的作用下E点逆时针转动, 直到F点由上连杆BC连线的右侧运动到BC连线的左侧, 主拉簧的弹簧力将使连杆BC绕C点顺时针转动, 并带动下连杆AB、动触头OA一起绕O点逆时针转动, 从而实现动、静触头合闸。

2 MCCB操作机构受力分析

MCCB操作机构有关的力学方面特性主要包括手柄再扣力、手柄合闸力、主拉簧力、触头终压力、脱扣力等。操作机构的这五种力极大地影响了产品的可靠性、稳定性, 因此对这些力的分析计算很有必要。

2.1 再扣操作力的计算

MCCB自由脱扣后, 即将再扣时, 以杠杆为研究对象, 以E点为力偶作用点对杠杆进行受力分析。自由脱扣状态杠杆受力分析如图3所示。

	Figure Option View Download New Window
	图3 自由脱扣状态杠杆受力分析

杠杆所受力在E点形成力偶平衡, 即

$F_{Z} L_{Z} = F_{TK} L_{TK} - F_{T} L_{T}$ (1)

式中: F_Z— — MCCB的再扣力;

F_TK— — 自由脱扣时跳扣对杠杆的作用力;

F_T— — 自由脱扣时主拉簧对杠杆的作用力;

L_Z— — MCCB的再扣力作用点到E点的距离;

L_TK— — 自由脱扣时跳扣对杠杆的作用力到E点的距离;

L_T— — 自由脱扣时主拉簧对杠杆的作用力到E点的距离。

MCCB自由脱扣后, 即将再扣时, 由于上连杆BC在再扣过程中的C点一直钩着跳扣杆DCG运动, 所以将跳扣杆与上连杆作为一个整体来研究, 称之为跳扣组件, 以D点为力偶作用点对跳扣组件进行受力分析。自由脱扣状态跳扣组件受力分析如图4所示。

	Figure Option View Download New Window
	图4 自由脱扣状态跳扣组件受力分析

跳扣所受力在D点形成力偶平衡, 即

$F_{G} L_{G} = F_{t} L_{t}$ (2)

式中: F_G— — 自由脱扣时杠杆对跳扣组件的作用力;

F_t— — 自由脱扣时主拉簧对跳扣组件的作用力;

L_G— — 自由脱扣时杠杆对跳扣组件的作用力到D点的距离;

L_t— — 自由脱扣时主拉簧对跳扣组件的作用力到D点的距离。

F_Tk与F_G、F_T与F_t为两对互为反作用力, 即

$F_{Tk} = F_{G}, F_{T} = F_{t}$ (3)

结合式(1)~式(3)可得再扣力:

$F_{Z} = F_{T} (\frac{L_{t} L_{TK}}{L_{G} L_{Z}} - \frac{L_{T}}{L_{Z}})$ (4)

2.2 合闸操作力的计算

MCCB再扣后, 即将合闸时, 以杠杆为研究对象, 以E点为力偶作用点对杠杆进行受力分析, 再扣状态杠杆受力分析如图5所示。

	Figure Option View Download New Window
	图5 再扣状态杠杆受力分析

杠杆所受力在E点形成力偶平衡, 即:

$F_{H} L_{H} = F_{g} L_{g}$ (5)

式中: F_H— — MCCB合闸力;

F_g— — 再扣时主拉簧对杠杆的作用力;

L_H— — 再扣时MCCB的再扣力的作用点到E点的距离;

L_g— — 再扣时主拉簧对杠杆的作用力到E点的距离。

由式(5)可得合闸操作力为

$F_{H} = \frac{F_{g} L_{g}}{L_{H}}$ (6)

2.3 主拉簧力的计算

MCCB在合闸的过程中, 动、静触头接触的瞬间, 以下连杆为研究对象, 以B点为力作用点进行受力分析, 主拉簧的力与分解到上、下连杆方向的力组成了一个三角形。动、静触头接触瞬间下连杆受力分析如图6所示。

	Figure Option View Download New Window
	图6 动、静触头接触瞬间下连杆受力分析

由正弦定理可得:

$\frac{F_{ab}}{\sin α} = \frac{F_{th}}{\sin β}$ (7)

式中: F_ab— — 动、静触头接触瞬间主拉簧作用在下连杆上的分力;

F_th— — 动、静触头接触瞬间主拉簧的拉力;

α — — MCCB的合闸角;

β — — MCCB的分闸角。

MCCB在合闸的过程中, 动、静触头刚刚接触的瞬间, 以动触头组件为研究对象, 动触头被触头扭簧压在转轴上, 因此将其看成一个整体来研究, 称其为动触头组件。以O点为力作用点对触头组件进行受力分析, 动、静触头接触瞬间动触头组件受力分析如图7所示。

	Figure Option View Download New Window
	图7 动、静触头接触瞬间动触头组件受力分析

触头组件的合闸力矩为

$M_{H} = F_{ba} L_{ba}$ (8)

式中: M_H— — 动、静触头刚接触瞬间触头组件合闸力矩;

F_ba— — 动、静触头刚接触瞬间下连杆对触头组件的作用力;

L_ba— — 动、静触头刚接触瞬间下连杆对触头组件的作用力到O点的距离。

触头组件的反力矩为

$M_{F} = 3 F_{0} L_{0}$ (9)

式中: M_F— — 动、静触头刚接触瞬间触头组件所受的反力矩;

F₀— — 动、静触头刚接触瞬间触头所受的作用力, 即初压力;

L₀— — 动、静触头刚接触瞬间触头所受的初压力到O点的距离。

对于三极MCCB, M_F=3F₀L₀, 对于四极MCCB, 则为4F₀L₀。经典三菱操作机构设计经验要求:

$M_{H} \geq 1.2 M_{F}$ (10)

F_ab互为F_ba为一组反作用力, 即

$F_{ab} = F_{ba}$ (11)

结合式(7)~式(11)可得主拉簧力为

$F_{th} = \frac{3.6 F_{0} L_{0}}{L_{ba}} \cdot \frac{\sin β}{\sin α}$ (12)

2.4 触头终压力的计算

MCCB处于完全合闸后, 以动触头为研究对象, 以O点为力偶作用点对动触头进行受力分析, 合闸状态动触头受力分析如图8所示。

	Figure Option View Download New Window
	图8 合闸状态动触头受力分析

动触头所受力在O点形成力偶平衡, 即

$F_{J} L_{J} = M_{D}$ (13)

式中: F_J— — 合闸后静触头施加给动触头的终压力;

M_D— — 合闸后触头扭簧施加给动触头的作用力距;

L_J— — 合闸后静触头施加给动触头的作用力到O点的距离。

由式(14)可得触头终压力为

$F_{J} = \frac{M_{D}}{L_{J}}$ (14)

2.5 脱扣力的计算

MCCB完全合闸后, 双金属片受热变形后即将推动再扣杆上的牵引杆时, 以再扣杆为研究对象, 以J点为力偶作用点对再扣杆进行受力分析。合闸状态再扣杆受力分析如图9所示。

	Figure Option View Download New Window
	图9 合闸状态再扣杆受力分析

再扣杆所受力在J点形成力偶平衡, 即

$F_{TKL} L_{TKL} = M_{Z} - F_{SK} L_{SK}$ (15)

式中: F_TKL— — MCCB的脱扣力;

M_Z— — 合闸后再扣扭簧施加给再扣杆的作用力;

F_SK— — 合闸后锁扣施加给再扣杆的作用力;

L_TKL— — MCCB的脱扣力到J点的距离;

L_SK— — 合闸后锁扣施加给再扣杆的作用力到J点的距离。

MCCB完全合闸后, 以锁扣为研究对象, 以I点为力偶作用点对锁扣进行受力分析, 合闸状态锁扣受力分析如图10所示。

	Figure Option View Download New Window
	图10 合闸状态锁扣受力分析

锁扣所受力在I点形成力偶平衡, 即

$F_{ZK} L_{ZK} = F_{tk} L_{tk} - M_{S}$ (16)

式中: F_ZK— — 合闸后再扣杆施加给锁扣的作用力;

F_tk— — 合闸后跳扣施加给锁扣的作用力;

M_S— — 合闸后锁扣扭簧施加给锁扣的作用力;

L_ZK— — 合闸后再扣杆施加给锁扣的作用力到I点的距离;

L_tk— — 合闸后跳扣施加给锁扣的作用力到I点的距离。

MCCB完全合闸后, 以跳扣为研究对象, 以D点为力偶作用点对跳扣进行受力分析, 合闸状态跳扣受力分析如图11所示。

	Figure Option View Download New Window
	图11 合闸状态跳扣受力分析

跳扣所受力在D点形成力偶平衡, 即

$F_{S} L_{S} = F_{BC} L_{BC}$ (17)

式中: F_S— — 合闸后锁扣施加给跳扣的作用力;

F_BC— — 合闸后上连杆施加给跳扣的作用力;

L_S— — 合闸后锁扣施加给跳扣的作用力到D点的距离;

L_BC— — 合闸后上连杆施加给跳扣的作用力到D点的距离。

MCCB完全合闸后, 以上连杆为研究对象, 以B点为力的作用点对上连杆进行受力分析, 合闸状态上连杆受力分析如图12所示。

	Figure Option View Download New Window
	图12 合闸状态上连杆受力分析

上连杆所受力在B点平衡, 即

$F_{CB} = F_{AB} \cos β + F_{TH} \cos α$ (18)

式中: F_CB— — 合闸后跳扣施加给上连杆的作用力;

F_AB— — 合闸后下连杆施加给上连杆的作用力;

F_TH— — 合闸后主拉簧施加给上连杆的作用力。

MCCB完全合闸后, 动触头被触头扭簧压在转轴上, 因此将其看成一个整体来研究, 称其为动触头组件, 以O点为力偶作用点对动触头组件进行受力分析。合闸状态动触头组件受力分析如图13所示。

动触头组件所受力在O点形成力偶平衡, 即

$F_{BA} L_{BA} = 3 F_{J} L_{J}$ (19)

	Figure Option View Download New Window
	图13 合闸状态动触头组件受力分析

式中: F_BA— — 合闸后下连杆施加给触头组件的作用力;

F_J— — 合闸后静触头施加给触头组件的终压力;

L_BA— — 合闸后下连杆施加给触头组件的作用力到O点的距离;

L_J— — 合闸后静触头施加给触头组件的终压力到O点的距离。

对于三极MCCB, F_BAL_BA=3F_JL_J; 对于四极MCCB, 则为4F_JL_J。F_Zk与F_SK, F_S与F_tk, F_CB与F_BC, F_BA与F_AB互为四对反作用力, 即

$F_{ZK} = F_{SK}, F_{S} = F_{tk}, F_{C B} = F_{BC}, F_{BA} = F_{AB}$ (20)

将式(14)~式(20)代入式(15), 脱扣力为

$\begin{array}{l} F_{TKL} = \frac{M_{Z}}{L_{TKL}} + \frac{F_{TH} \cos α L_{BC} L_{tk} L_{SK}}{L_{S} L_{ZK} L_{TKL}} - \\ \frac{3 M_{D} \cos β L_{BC} L_{tk} L_{SK}}{L_{BA} L_{S} L_{ZK} L_{TKL}} - \frac{M_{S} L_{SK}}{L_{ZK} L_{TKL}} \end{array}$ (21)

3 结语

本文从MCCB操作机构的静态特性及运动原理特性, 详细阐述了MCCB分闸、合闸、自由脱扣过程, 分析研究了操作机构在稳定状态和特殊瞬态各杆件的受力情况, 给出了MCCB五大关键力参数:再扣力、合闸力、主拉簧力、终压力、牵引杆脱扣力的计算方法及公式, 可以得出如下结论:

(1)MCCB的再扣力和合闸力均与机构主拉簧成正比关系。

(2)MCCB操作机构主拉簧力至少应大于触头弹簧反力(3F₀, 三极MCCB)的1.2倍, MCCB

才能可靠合闸, 同时主拉簧力与合闸角成反比, 与分闸角成正比。

(3)MCCB触头终压力与触头扭簧成正比, 与动、静触头接触点到动触头的旋转中心成反比, 增大触头的扭簧, 可以直接通过调整触头扭簧力值来满足要求的触头终压力。

(4)MCCB操作机构设计时, 可以通过调整弹簧拉力、各杆件长度、各支点相互位置、各杆件接触点限位位置等来达到相应的力学要求。

(5)通过MCCB脱扣力可以反向推出双金属片、电磁系统所需的动力。

参考文献

文献列表

[1]	赵科达, 胡昌勇, 张亦威, 等. 一种新的电子式塑壳断路器的后备保护装置[J]. 电器与能效管理技术, 2019(21): 25-28. [本文引用:1]
[2]	周宏明, 沈艳, 黄沈权, 等. 塑壳式断路器操作机构的动力学模型及性能分析[J]. 计算机集成制造系统, 2015(5): 1350-1358. [本文引用:1]
[3]	陈德桂, 刘庆江, 康艳. 塑壳断路器操作机构分断速度的影响因素[J]. 低压电器, 2005(12): 9-12. [本文引用:1]
[4]	蒋顾平, 顾惠民. 提高塑壳断路器操作机构动作速度的研究[J]. 电器与能效管理技术, 2015(1): 21-23. [本文引用:1]
[5]	苏秀萍, 任俊勇, 刘金鹿, 等. 基于ADAMS的塑壳式断路器操作机构可靠性分析[J]. 低压电器, 2010(12): 1-4. [本文引用:1]

2019

0.0

... MCCB主要部件包括操作机构、触头系统、灭弧系统等,操作机构作为MCCB的执行机构,更是MCCB整个系统的核心机构^[1] ...

2015

0.0

... 周宏明等^[2]通过采用拉格朗日方程建立了断路器操作机构的动力学模型,分析了操作机构的等效转动惯量和广义作用力 ...

2005

0.0

陈德桂, 刘庆江, 康艳. 塑壳断路器操作机构分断速度的影响因素[J]. 低压电器, 2005(12): 9-12.

操作机构的动态特性是决定低压塑壳断路器分断性能的重要因素.采用多体动力学方法仿真塑壳断路器机构的分断过程,并用实验加以验证.在此基础上,仿真分析了各种结构参数对断路器操作机构分断速度的影响,包括分断弹簧、各连杆的转轴位置等.

... 陈德桂等^[3]通过建立简化的三维模型,对操作机构的弹簧刚度、分断时间和分断速度进行了深入分析 ...

2015

0.0

... 蒋顾平等^[4]通过三维建模仿真,分析了操作机构的关键轴位置、杆件质量、连杆转化位置对操作机构动作速度的影响 ...

2010

0.0

苏秀萍, 任俊勇, 刘金鹿, 等. 基于ADAMS的塑壳式断路器操作机构可靠性分析[J]. 低压电器, 2010(12): 1-4.

在分析与智能塑壳式断路器配套使用的铁心电流互感器的结构原理及传统设计基础上,提出了一种新的有取向硅钢片代替无取向硅钢片的优化设计.采用纵向增加补偿硅钢片,有效补偿纵向硅钢片导磁截面积不足;利用条形硅钢片之间特定的衔接方式,解决条型硅钢片固定困难的问题;合理改进硅钢片加工工艺,以提高其取向性.该优化设计在不增加电流互感器体积的前提下,大大提高其抗磁饱和能力,更加满足智能塑壳式断路器的测量范围和保护精度.

... 苏秀萍等^[5]采用有限元分析法对MCCB连杆机构的可靠性进行了分析 ...