主动配电网源-网-荷双层两阶段优化调度

引用本文

李继宇, 江修波, 李功新, 范映. 主动配电网源-网-荷双层两阶段优化调度[J]. 电器与能效管理技术, 2020(1): 78-85.
LI Jiyu, JIANG Xiubo, LI Gongxin, FAN Ying. Two-Stage Optimal Dispatching of Active Distribution Network with Two Layers of Source-Network-Load[J]. ELECTRICAL & ENERGY MANAGEMENT TECHNOLOGY, 2020(1): 78-85.
Doi:10.16628/j.cnki.2095-8188.2020.01.013 复制到剪切板

Permissions

《电器与能效管理技术》编辑部所有

主动配电网源-网-荷双层两阶段优化调度

李继宇¹, 江修波¹, 李功新^1,², 范映³

1.福州大学电气工程与自动化学院, 福建福州 350108

2.国网福建省电力有限公司, 福建福州 350003

3.国网福建省电力有限公司检修分公司, 福建福州 350013

作者简介：

李继宇(1992—),男,硕士研究生,研究方向为电力系统规划与调度。
江修波(1960—),男,教授,研究方向为电力系统运行及管理、电力设备绝缘诊断。
李功新(1964—),男,博士,教授级高级工程师,主要从事电力系统自动化运行及管理研究。

收稿日期: 2019-10-13

摘要

为实现主动配电网(ADN)中风、光分布式发电(DG)的充分消纳,促进储能装置及柔性负荷等可控资源的高效利用,提出基于源-网-荷的双层两阶段优化调度。日前双层优化调度阶段上层为有功优化调度,下层为将DG作为无功输出源的无功优化调度,采用二进制混沌蝙蝠算法进行求解;实时调度阶段采用改进数据流在线分割的超短期预测,对日前调度方案进行实时修正。最后,采用修改后的IEEE-33节点系统作为算例,验证了调度方案的有效性。

关键词: 主动配电网; 双层优化; 实时修正; 两阶段调度; 需求侧管理

中图分类号:TM73 文献标志码:A 文章编号:2095-8188(2020)01-0078-08 doi: 10.16628/j.cnki.2095-8188.2020.01.013

Two-Stage Optimal Dispatching of Active Distribution Network with Two Layers of Source-Network-Load

LI Jiyu¹, JIANG Xiubo¹, LI Gongxin^1,², FAN Ying³

1.College of Electrical Engineering and Automation,Fuzhou University, Fuzhou 350108, China

2.Fujian Electric Power Company Limited,Sate Grid, Fuzhou 350003, China

3.Maintenance Branch Company of Fujian Electric Power Co.,Ltd., State Grid, Fuzhou 350013, China

Abstract

In order to fully absorb apoplexy and optical DG in active distribution network (ADN) and promote the efficient utilization of controllable resources such as energy storage devices and flexible loads,a two-layer two-stage optimal dispatch based on source-network-load was proposed.In the previous two-tier optimal dispatching stage,the upper level is active power optimal dispatching,and the lower level is reactive power optimal dispatching with DG as reactive power output source,which is solved by binary chaotic bat algorithm.In the real-time dispatching stage,ultra-short-term prediction based on improved data stream on-line segmentation is used to revise the previous dispatching scheme in real time.Finally,a modified IEEE-33 bus system is used as an example to verify the effectiveness of the scheduling scheme.

Keyword: active distribution network; double layer optimization; real-time correction; two-stage scheduling; demand side management

文章图片

0 引言

随着分布式发电(Distributed Generation, DG)技术的成熟, 使得DG的应用得到巨大推广, 合理容量的DG并网能够降低系统损耗, 改善电能质量以及提高系统可控性^{[1, 2, 3]}。目前, 大电网与DG相结合是未来电力系统的发展趋势, 将合理的负荷预测结果及先进的在线监测技术相融合, 进而科学合理地对DG进行优化调度, 能够使接入的DG、储能装置及无功补偿装置等发挥最大效益, 确保配电网清洁、经济、稳定运行。

目前, 国内对于含DG配电网的主要研究放在供电质量、可靠性、继电保护以及DG的规划上^{[4, 5, 6]}, 在经济性调度上还有所欠缺。文献[7]针对“ 源-网-荷” 三者联合协调提出了一种包含DG、储能、柔性负荷控制的调控方法, 从电网公司利益出发构建了考虑购电成本、网络损耗及需求侧管理的综合调度模型, 并用改进的和声算法进行求解。文献[8]提出了空间和时间尺度全局协调优化的调度模型, 通过分布自治、分解协调机制开发了综合优化调度系统。文献[9, 10]分别提出日前两阶段及双层优化调度模型, 力求达到系统运行经济性最高。文献[11, 12]通过需求侧响应来降低用电成本。文献[13, 14]通过网络重构来使调度模型经济性达到最高。文献[15]提出一种动态-遗传算法的混合储能系统实时协调调度方案, 能够对调度方案进行实时修正, 但其实时修正阶段采用储能系统进行柔性控制, 使电网投资成本加大。

本文提出一种日前、日中相结合的两阶段优化调度方法, 包括日前优化调度阶段及实时修正阶段。日前优化阶段采用双层能量优化, 上层优化层日前调度成本最低为目标函数进行DG出力及购电的预调度, 下层优化层采用有功网损最低为目标函数进行无功优化; 日中实时修正阶段采用改进数据流在线分割的超短期预测获得最新预测数据后, 对日前调度方案进行实时修正。

1 主动配电网源-网-荷双层两阶段优化调度模型

主动配电网的双层优化调度模型建立在双层能量优化的基础上, 在充分考虑环境效益、运行条件及整体经济性的基础上, 通过主动管理措施对DG进行相关控制以达到调度成本最低及系统有功网损最低, 从而实现电网公司的效益最大化。

1.1 上层有功优化调度模型

(1) 目标函数。在日前有功优化阶段的目标函数为日前运行成本最低, 其具体目标函数:

$\begin{array}{l} F = \overset{T}{\sum_{t = 1}} \overset{N_{FI}}{\sum_{i = 1}} ρ^{FI} P_{i, t}^{FI} + \overset{T}{\sum_{t = 1}} ρ^{grid} P_{t}^{grid} + \\ \overset{T}{\sum_{t = 1}} \overset{N_{DG}}{\sum_{i = 1}} (ρ^{DG} P_{i, t}^{DG} - ξ P_{i, t}^{DG} + Z_{i, t} C_{off}) \end{array}$ (1)

式中: T— — 调度时段数;

N_FI— — 系统中柔性负荷总数量;

ρ ^FI— — 柔性负荷补偿单价;

$P_{i, t}^{FI}$ — — t时段第i户柔性负荷可削减量;

ρ ^grid— — 大电网购电单价;

$P_{t}^{grid}$ — — t时段供电公司购电量;

ρ ^DG— — DG运行维护成本;

$P_{i, t}^{DG}$ — — t时段第i台DG的有功出力;

ξ — — 政府补贴清洁能源发电收入;

Z_i_,_t— — t时段第i台DG的启停状态;

C_off— — DG关停成本。

(2) 约束条件。

①有功平衡约束:

$P_{t}^{Q} = \overset{N_{DG}}{\sum_{i = 1}} P_{i, t}^{DG} + \overset{N_{FI}}{\sum_{i = 1}} P_{i, t}^{FI} + P_{t}^{grid}$ (2)

式中: $P_{t}^{Q}$ — — t时段系统有功总量。

②DG出力上下限约束:

$P_{i}^{\min} \leq P_{i, t}^{DG} \leq P_{i}^{\max}$ (3)

式中: $P_{i}^{\min}$ 、 $P_{i}^{\max}$ — — 第i台DG出力的最小值及最大值。

③DG启停时间约束:

$\{\begin{array}{l} \overset{T_{mup, i}}{\sum_{k = 1}} U_{i, t - k + 1} \geq T_{mup, i} \\ \overset{T_{mdown}}{\sum_{k = 1}} (1 - U_{i, t - k + 1}) \geq T_{mdown, i} \end{array}$ (4)

式中: U_i_,_t— — 第i台DG在t时段运行状态, 取值为0或1, 1表示DG运行状态, 0表示关停状态;

T_mup,_i、T_mdown,_i— — 第i台DG的最小启动时间、关停时间。

④DG爬坡约束:

$\{\begin{array}{l} P_{i, t}^{DG} - P_{i, t - 1}^{DG} \leq U p_{i} Δ t, 上爬坡 \\ P_{i, t - 1}^{DG} - P_{i, t}^{DG} \leq Dow n_{i} Δ t, 下爬坡 \end{array}$ (5)

式中: $P_{i, t}^{DG}$ 、 $P_{i, t - 1}^{DG}$ — — 第i台DG在t时段、t-1时段的有功出力量;

Up_i、Down_i— — 第i台DG上、下爬坡率最值。

⑤联络线功率约束:

$|P_{t}^{grid}| \leq P_{\max}^{grid}$ (6)

式中: $P_{\max}^{grid}$ — — 联络线有功传输最大值。

⑥系统旋转备用约束:

$\overset{N_{DG}}{\sum_{i = 1}} P_{i, \max}^{DG} U_{i, t} + \overset{N_{FI}}{\sum_{j = 1}} P_{j, \max}^{FI} I_{j, t} + P_{t}^{grid} + R_{t} \geq P_{t}^{Q}$ (7)

式中: $P_{i, \max}^{DG}$ — — 第i台DG在t时段最大有功出力;

$P_{j, \max}^{FI}$ — — 第j个柔性负荷最大可中断负荷量;

I_j_,_t— — t时段第j个柔性负荷是否切负荷, 取值为0或1, 1表示切负荷, 0表示不切负荷;

R_t— — t时段的备用负荷。

⑦储能装置约束:

$SO C_{\min} \leq SOC \leq SO C_{\max}$ (8)

式中: SOC_max、SOC_min— — 电池荷电状态的最大值和最小值。

1.2 下层无功优化调度模型

光伏、风力发电的DG不仅能够输出有功功率, 同时也能够输送一定容量的无功功率, 合理利用其无功输出, 能够起到对电网的无功优化作用。其中光伏能够提高的无功功率容量:

${|Q_{g}|}_{\max} (t) = \sqrt[]{S_{\max}^{2} - P_{act}^{2} (t)}$ (9)

式中: Q_g— — 光伏输出无功功率;

S_max— — 光伏机组所能提供最大视在功率;

P_act— — 光伏机组输出有功功率。

双馈风机的无功输出:

$\begin{array}{l} - \frac{3 U_{1}^{2}}{X_{1}} - \sqrt[]{(\frac{3 X_{m} U_{1}}{X_{1}} I_{r \max})^{2} - P_{w}^{2}} \leq Q_{s} \leq \\ \sqrt[]{(\frac{3 X_{m} U_{1}}{X_{1}} I_{r \max})^{2} - P_{w}^{2}} \end{array}$ (10)

式中: Q_s— — 风机输出无功功率;

U₁— — 风机定子电压;

X₁— — 风机定子电抗;

X_m— — 风机励磁电抗;

I_r_max— — 风机转子最大电流;

P_w— — 风机输出有功功率。

随着风机输出有功功率增大, 无功调节范围缩小, 调节能力降低。

(1) 目标函数。日前无功优化以系统有功网损及加权电压偏移率最低为目标函数, 具体目标函数:

$C_{lost} = \min [\overset{N_{L}}{\sum_{i = 1}} P_{i, lost} + δ \overset{N_{B}}{\sum_{j = 1}} (1 - \frac{U_{N} - U_{j}}{U_{N}})]$ (11)

式中: P_i_{, lost}— — 系统第i个支路的网损值;

N_L— — 系统总支路数;

δ — — 加权系数;

U_N— — 系统基准电压值;

U_j— — 第j节点电压值;

N_B— — 系统总节点数。

(2) 约束条件。

①潮流约束:

$P_{i}^{grid} + P_{i}^{DG} + P_{i}^{FI} - {P^{L}}_{i} = \sum_{j} |U_{i}| |U_{j}| |Y_{ij}| \cos (θ_{ij} + δ_{j} - δ_{i})$ (12)

$Q_{i}^{grid} + Q_{i}^{DG} + Q_{i}^{FI} - {Q^{L}}_{i} = \sum_{j} |U_{i}| |U_{j}| |Y_{ij}| \sin (θ_{ij} + δ_{j} - δ_{i})$ (13)

式中: U_i、U_j— — 系统第i、j节点的节点电压值;

$P_{i}^{grid}$ 、 $P_{i}^{DG}$ 、 $P_{i}^{FI}$ 、 ${P^{L}}_{i}$ — — 系统第i节点电网注入有功值、DG注入有功值、柔性负荷切出有功值及负荷消纳有功值;

$|Y_{ij}|$ — — 第i、j节点之间支路的电导值;

θ _ij— — Y_ij的相角值;

δ _i、δ _j— — 系统第i、j节点的节点电压相角值;

$Q_{i}^{grid}$ 、 $Q_{i}^{DG}$ 、 $Q_{i}^{FI}$ 、 ${Q^{L}}_{i}$ — — 系统第i节点电网注入无功值、DG注入无功值、无功补偿器注入无功值及负荷所需无功值。

②DG无功出力约束:

$Q_{i, \min}^{DG} \leq Q_{i}^{DG} \leq Q_{i, \max}^{DG}$ (14)

式中: $Q_{i, \min}^{DG}$ 、 $Q_{i, \max}^{DG}$ — — 第i台DG无功出力的最小值及最大值。

③无功补偿器出力约束:

$Q_{i, \min}^{S} \leq Q_{i}^{S} \leq Q_{i, \max}^{S}$ (15)

式中: $Q_{i, \min}^{S}$ 、 $Q_{i, \max}^{S}$ — — 第i台无功补偿器容量的下限值及上限值。

④节点电压约束:

$U_{i, \min} \leq U_{i} \leq U_{i, \max}$ (16)

式中: U_i_{, min}、U_i_{, max}— — 第i个节点节点电压的下限值、上限值。

1.3 源-网-荷双层优化调度模型

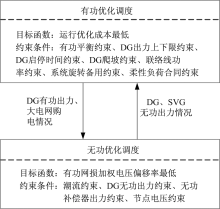
主动配电网的双层优化调度模型建立在双层能量优化的基础上, 通过主动管理措施对DG进行相关控制, 以达到调度成本最低及系统有功网损最低, 从而实现电网公司的效益最大化。有功-无功双层调度优化模型如图1所示。

	Figure Option View Download New Window
	图1 有功-无功双层调度优化模型

本文从环境、运行及经济性角度出发, 以能量交互、电网运行及负荷侧响应为基础, 构建源-网-荷双层优化调度模型。上层模型以运行成本最低为目标函数, 综合源-网-荷情况, 最终确定DG有功出力情况及大电网购电计划, 将其传递给下层调度模型; 下层调度模型以有功网损及加权电压偏移率最低为目标函数, 对系统进行无功优化, 确定DG及无功补偿器的无功出力情况, 并将其反馈给上层调度模型, 通过各层调度模型最优策略的传递及反馈, 从而计算出符合整体最优运行的优化结果。

2 实时调度修正阶段

2.1 修正阶段有功处理

日前调度的风、光出力及负荷情况是基于预测数据, 与真实数据存在一定误差。由于日前采用的是短期预测, 相较于超短期预测, 后者拥有更高精度, 对实时调度情况作出更优决策。本文采用基于改进数据流在线分割的超短期预测^[16]对风、光出力及负荷情况进行超短期预测。

由于风速、光照强度短期预测值与超短期预测值存在偏差, 对日前调度结果进行实时修正方能使系统达到最优, 其大电网购电量功率修正:

$Δ P_{t}^{grid} = P_{t}^{grid} - P_{t, s}^{grid}$ (17)

$P_{t, s}^{grid} = Δ P_{t}^{PV, WG} + Δ P_{t}^{FI}$ (18)

$Δ P_{t}^{PV, WG} = \overset{N_{PV}}{\sum_{i = 1}} (P_{t}^{PV} - P_{t, s}^{PV}) + \overset{N_{WG}}{\sum_{i = 1}} (P_{t}^{WG} - P_{t, s}^{WG})$ (19)

$Δ P_{t}^{FI} = \{\begin{array}{l} 0, P_{t}^{FI} + Δ P_{t}^{PV, WG} \leq P_{t, \max}^{FI} \\ P_{t}^{FI} + Δ P_{t}^{PV, WG} - P_{t, \max}^{FI}, P_{t}^{FI} + Δ P_{t}^{PV, WG} > P_{t, \max}^{FI} \end{array}$ (20)

式中: Δ $P_{t}^{grid}$ — — 大电网购电变化量;

$P_{t, s}^{grid}$ — — 超短期预测下大电网购电量。

Δ $P_{t}^{PV, WG}$ — — 短期预测与超短期预测风、光出力变化量;

Δ $P_{t}^{FI}$ — — 柔性负荷功率修正量;

$P_{t, s}^{WG}$ 、 $P_{t, s}^{PV}$ — — 超短期预测风、光出力;

$P_{t, \max}^{FI}$ — — t时刻柔性负荷最大值。

2.2 修正阶段重新计算

双层优化调度模型在优化结果上相较于多目标优化调度模型而言能够对调度方案进行更进一步优化, 但双层优化采用双层嵌套, 在计算时间上劣势明显。本文采用超短期负荷对风、光、荷情况进行预测, 力求达到最小误差, 从而提高可再生清洁能源的最大利用率, 预测周期为1 h; 但由于双层模型计算过程复杂, 耗时过长, 导致可能无法及时得出最新调度结果对日前方案进行修正。因此在实时修正之前先对超短期预测情况与日前短期预测情况进行修正评估。具体评估方法如下:

$Ψ = \{\begin{array}{l} 0, \frac{Δ P_{t}^{PV} + Δ P_{t}^{WG} + Δ {P^{L}}_{t}}{P_{t}^{PV} + P_{t}^{WG} + {P^{L}}_{t}} \leq γ \\ 1, \frac{Δ P_{t}^{PV} + Δ P_{t}^{WG} + Δ {P^{L}}_{t}}{P_{t}^{PV} + P_{t}^{WG} + {P^{L}}_{t}} > γ \end{array}$ (21)

式中: Ψ — — 修正评估后结果, 0表示不进行修正, 1表示进行实时修正;

γ — — 设置的误差系数比例。

根据实时修正评估结果, 当评估结果为需要修正时, 采用多目标优化算法设定综合运行成本最低、有功网损及加权电压偏移率最低为目标进行寻优; 当评估结果为不进行修正时, 采用日前双层调度结果对系统进行运行控制。

3 模型求解

3.1 二进制混沌蝙蝠优化算法

本文采用混沌蝙蝠算法^[17]对模型进行求解。由于本文模型中增加DG机组的启停情况, 即增加了0-1变量。为了适应ADN源-网-荷的协调优化的更高要求, 本文在混沌蝙蝠优化算法的基础上, 引入二进制化, 从而提高算法的适应性, 对包含离散变量的优化问题有更进一步的延伸。

二进制混沌蝙蝠优化算法在迭代过程中, 每个个体的位置取0或1, 而其他的迭代公式与混沌蝙蝠优化算法相同。每次迭代过程中, 第i只蝙蝠在d维的离散化公式:

$u_{i}^{d} = \{\begin{array}{l} 1, sigmoid (x_{i}^{d}) > rand \\ 0, sigmoid (x_{i}^{d}) \leq rand \end{array}$ (22)

$sigmoid (x_{i}^{d}) = \frac{1}{1 + e^{- x_{i}^{d}}}$ (23)

式中: $u_{i}^{d}$ — — 第i只蝙蝠在d维的新位置, 即DG机组的启停状态;

$x_{i}^{d}$ — — 第i只蝙蝠原有位置, 即第i台DG的输出功率。

3.2 模型求解步骤

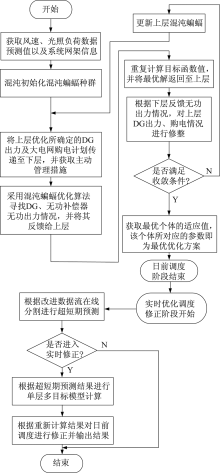
结合混沌蝙蝠优化算法的相关内容, 双层两阶段优化求解流程如图2所示。

	Figure Option View Download New Window
	图2 双层两阶段优化求解流程

步骤1:基础数据及算法的基本参数初始化, 如混沌蝙蝠优化算法的迭代次数、初始种群数量、Tent混沌序列迭代次数等。

步骤2:初始化规划层蝙蝠种群, 并将其引入Tent混沌序列, 利用适应度函数对步骤1所产生的个体进行优劣评价, 并找出最优位置个体。

步骤3:利用本文所提的方法将个体的位置二进制化, 将离散变量目标函数引入个体蝙蝠中, 检验DG启停及有功/无功输出情况的优劣。

步骤4:将上层DG出力情况方案传递至下层, 以上层传递结果初始化下层, 并针对此结果进行无功优化, 将DG、无功补偿器无功出力情况反馈至上层。

步骤5:根据下层DG、无功补偿器无功出力情况, 对上层DG有功出力、大电网购电情况进行修整。

步骤6:判断是否满足输出要求, 若满足终止迭代要求, 输出日前优化调度方案; 若不满足, 返回步骤4循环操作。

步骤7:进入实时调度方案修正阶段, 采用改进数据流在线分割进行超短期负荷预测。

步骤8:判断是否进行实时修正。若满足实时修正条件, 则进行多目标实时修正阶段; 若不满足实时修正条件, 则输出日前优化调度结果。

4 算例分析

4.1 算例基本参数

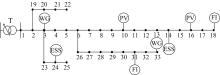
基于IEEE-33节点配电系统, 对其进行主动改造。修改后IEEE-33节点配电系统如图3所示。

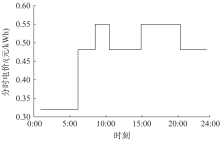
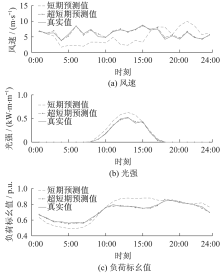
	Figure Option View Download New Window
	图3 修改后IEEE-33节点配电系统

图3中, 经过主动改造后的IEEE-33节点配电系统电压等级为12.66 kV; PV、WG、ESS、FI分别表示分布式光伏发电、分布式风力发电、储能装置及柔性负荷; 在10号、16号节点接入PV, 在3号、33号节点接入WG, 在14号、24号节点分别接入ESS, 在18号、31号节点分别接入FI; 各类能源的最优配置方案如表1所示。大电网购电成本中峰、谷电价分别为0.55元/kWh、0.33元/kWh, 平时电价为0.488元/kWh, 全天分时电价曲线如图4所示; 政府对风、光发电的环保正向激励为0.2元/kWh。全天风速、光强及负荷标幺值曲线如图5所示。

表1 各类能源的最优配置方案

	Figure Option View Download New Window
	图4 全天分时电价曲线

	Figure Option View Download New Window
	图5 全天风速、光强及负荷标幺值曲线

4.2 算例结果分析

对二进制混沌蝙蝠算法进行参数设置, 将种群规模设置为50, 最大迭代次数设置为100次, γ 修正比例设置为0.02, 对源-网-荷双层调度模型进行求解, 分析如下:

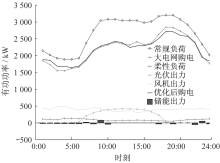
(1) 具体调度情况分析。系统全天有功调度结果如图6所示。

	Figure Option View Download New Window
	图6 系统全天有功调度结果

由图6可知, 日前优化调度和实时修正调度系统各时段总购电量分别为53.727 MW及51.387 MW, 在大电网购电量上由于实时修正调度最大限度降低弃风、弃光的出现, 在总购电量成本上有一定减少, 且从曲线看来实时进行超短期DG出力及负荷预测能够使整体曲线更加平滑, 整体平稳得到一定提升。因需求侧存在可调度柔性负荷, 能够给日前调度阶段预测出现的较大误差提供一定裕量进行修正补偿。由于短期预测对风、光出力进行预测存在较大误差, 导致弃光弃风的现象出现, 在使用超短期预测后能够大幅度提高预测精度, 使风、光使用率大大提高。储能系统主要在常规负荷处于低位时进行充电, 在用电高峰期进行放电, 从而起到削峰填谷作用^[18]。

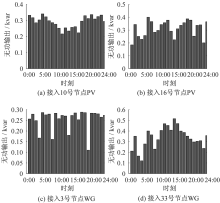
系统全天DG无功出力调度结果如图7所示。当PV及WG作为无功源输出之后, 能够大幅度减小对电网及无功补偿器无功值的需求, 从而得到防止网络堵塞, 降低整体网络损耗的目的。

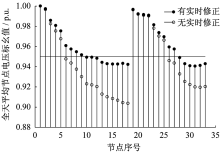
	Figure Option View Download New Window
	图7 系统全天DG无功出力调度结果

(2) 节点电压分析。全天24 h下, 若采用无实时修正及超短期负荷预测实时修正, 系统全天

节点平均电压如图8所示。

	Figure Option View Download New Window
	图8 系统全天节点平均电压

由图8可知, 若系统采用短期预测后进行调度, 由于真实值和日前调度所用的预测值有较大误差, 导致最低节点电压低至0.903 7 p.u.; 而采用超短期预测与真实值具有极高精度, 其节点最低电压为0.942 5 p.u., 使系统整体电压偏移率大大降低, 使用户用电满意度得到一定保障。使用短期日前调度策略中整体节点电压低于0.95 p.u.节点达到21个, 超过系统全局60%; 采用超短期预测实时修正的情况下, 整体低于0.95 p.u.节点数仅为系统末端的12个节点, 能够使全局系统都处于较低电压偏移率。综上分析, 证实了本文所涉及的源-网-荷双层两阶段调度方法的有效性及合理性。

(3) 整体经济性分析。本文所构建的源-网-荷双层两阶段优化调度旨在构建用户满意度、环境友好度、电能质量高和网络损耗、系统波动、运行成本低的调度方案。采用短期预测日前调度及超短期预测实时修正调度相结合, 来进行主要经济成本分析。不同调度方案的经济指标对比如表2所示。

表2 不同调度方案的经济指标对比

由表2可知, 采用超短期预测实时修正调度的清洁能源利用率能够达到96.77%, 对短期风、光及负荷预测带来的误差能够进行最大程度的修正; 在清洁能源利用及柔性负荷裕量使用上能够最大限度协调, 超短期预测实时修正调度在各项费用上都有明显优势, 在当日运行总成本上较短期负荷预测降低0.203 1万元, 降幅达到7.70%; 比较于经济调度模型, 总成本降低0.508 5万元, 降幅达到17.29%。综合各项指标, 本文提出源-网-荷双层两阶段优化调度方案能使各项指标达到优化。

5 结语

对主动配电网双层两阶段调度模型进行研究, 所得结论如下:

(1) 配电系统规划时, 往往采用长期负荷预测对其进行容量的选取, 但在系统运行时往往风、光出力及负荷使用情况等存在较大误差, 因此规划时留有一定裕量。在日前进行调度方案制定时, 由于短期风、光出力及负荷仍与实际存在一定误差, 而超短期预测的精度较高, 因此实时修正调度方案能够最大程度减少弃风、弃光现象的出现。

(2) 实时修正调度能够充分协调DG、储能装置及柔性负荷的作用, 在负荷曲线上, 对系统负荷曲线起到削峰填谷的效果, 从而平抑负荷波动, 增强系统稳定性; 在系统运行上, 能够使系统最优化运行, 从而减小网损, 提高电能质量; 在经济指标上, 由于最大限度使用清洁能源发电, 使系统整体运行成本得到有效降低。

(3) 将DG作为无功源输出, 能够充分发掘设备潜力, 减少整体电网投资。虽然DG作为不可控出力, 但日前采用短期预测调度结合超短期预测实时修正, 能够极大限度地发掘DG的良性作用。

参考文献

文献列表

[1]	刘广一, 张凯, 舒彬. 主动配电网的6个主动与技术实现[J]. 电力建设, 2015, 36(1): 33-37. [本文引用:1]
[2]	SINGH B, MUKHERJEE V, TIWARI P. GA-based multi-objective optimization for distributed generations planning with DLMs in distribution power systems[J]. Journal of Electrical Systems and Information Technology, 2016, 4(1): 62-94. [本文引用:1]
[3]	ZHANG S X, CHENG H Z, LI K, et a1. Optimal siting and sizing of intermittent distributed generators in distribution system[J]. IEEE Transactions on Electrical and Electronic Engineering, 2015, 10: 628-635. [本文引用:1]
[4]	王红星, 王俊, 官国飞, 等. 分布式电源消纳电能质量影响及其权重分析[J]. 电力电容器与无功补偿, 2019, 40(3): 177-181. [本文引用:1]
[5]	李哲, 刘澄, 周杨, 等. 用户侧分布式电源对配电网电流保护的影响[J]. 广东电力, 2019, 32(3): 81-87. [本文引用:1]
[6]	刘伟生, 王蕾, 任杰, 等. 分布式电源接入的配电系统电压估算方法研究[J]. 电器与能效管理技术, 2018(2): 43-50. [本文引用:1]
[7]	廖剑波, 李振坤, 符杨. “源-网-荷”相协调的主动配电网经济调度[J]. 电力系统及其自动化学报, 2018, 30(1): 69-75. [本文引用:1]
[8]	杜红卫, 鲁文, 赵浚婧, 等. 城市配电网源网荷互动优化调度技术研究与应用[J]. 供用电, 2016, 33(1): 45-50. [本文引用:1]
[9]	林威, 孟宪君, 靳小龙, 等. 计及不同主体的配电网-微电网日前联合优化调度方法[J]. 供用电, 2018, 35(7): 9-12, 33. [本文引用:1]
[10]	陈乃仕, 鲁丹丹, 董雷, 等. 基于双层优化理论的交直流配电网调度研究[J]. 供用电, 2016, 33(8): 32-36. [本文引用:1]
[11]	GOUDARZI H, HATAMI S, PEDRAM M. Demand -side load scheduling incentivized by dynamic energy prices[C]//Smart Grid Communications. Brussels, Belgium, IEEE, 2011: 351-356. [本文引用:1]
[12]	GATSIS N, GIANNAKIS G B. Residential load control: distributed scheduling and convergence with lost AMI messages[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 770-786. [本文引用:1]
[13]	邢海军, 孙欣, 洪绍云. 考虑不同变电站电压差异的配电网重构[J]. 电力建设, 2018, 39(3): 65-70. [本文引用:1]
[14]	ELDURSSI A M, O'CONNELL R M. A Fast nondominated sorting guided genetic algorithm for multi-objective power distribution system reconfiguration problem[J]. IEEE Transactions on Power Systems, 2015, 30(2): 593-601. [本文引用:1]
[15]	朱永强, 王甜婧, 许阔, 等. 基于动态规划-遗传算法的混合储能系统实时协调调度和经济运行[J]. 太阳能学报, 2019, 40(4): 1059-1066. [本文引用:1]
[16]	唐聪岚, 卢继平, 谢应昭, 等. 基于改进数据流在线分割的超短期负荷预测[J]. 电网技术, 2014, 38(7): 2014-2020. [本文引用:1]
[17]	马迎东, 王文栋, 温强. 基于混沌搜索策略蝙蝠算法的输电网规划[J]. 电力系统保护与控制, 2015, 43(15): 17-21. [本文引用:1]
[18]	高辉, 虞小辉, 曹佳男. 多类型电源接入的配电网分层优化运行控制研究[J]. 电器与能效管理技术, 2018(20): 8-14. [本文引用:1]

2015

0.0

刘广一, 张凯, 舒彬. 主动配电网的6个主动与技术实现[J]. 电力建设, 2015, 36(1): 33-37.

This paper proposed six actives and key technologies of active distribution network, which are active planning, active management, active control and active service from the distribution grid side, active response from the customer side and active participation from the distributed generation side. On the side of grid companies, the active planning of distributed renewable energy, the organic coordination of planning and operation, the active management and control of distributed generation, the active service for superior power grid and users are emphasized. Under the conditions of ensuring the safe and stable operation of power grid, the active planning, management and control can increase the hosting capacity for the distributed renewable energy power generation. The active service can provide new opportunities for innovation of distribution network business model and expanding business areas. On the side of users, the responsibility of energy conservation and emissions reduction is emphasized. On the side of renewable generation, the effect of distribution generation sets on the network is emphasized, and the technologies of active power control and reactive power voltage regulation should be deployed to participate in the power grid dispatching operation. Finally, the technology of active distribution network is discussed based on the above analysis, including integrated planning technology, operation and control technology, technology of response of demand and technology of power control of renewable energy.

1. China Electric Power Research Institute, Beijing 100192, China； 2.Beijing Economic Technology Research Institute, Beijing 100055, China

提出了主动配电网（active distribution networks，ADN）的6个主动，即电网公司侧的主动规划、主动管理、主动控制与主动服务及用户侧的主动响应和分布式可再生能源发电侧的主动参与。在电网公司侧，强调对分布式可再生能源进行主动规划、对分布式发电进行主动管理和控制、对上级电网和用户提供主动服务。电网公司的主动规划、主动管理和主动控制可以在确保电网安全稳定运行的条件下，增强对分布式可再生能源发电的消纳能力；主动服务可以为配电网创新商业模式、扩展业务领域提供新的机遇。在用户侧，强调广大用户在力所能及的范围内，承担节能减排的责任，积极响应各种不同形式的需求侧激励措施。在分布式可再生能源发电侧，应充分考虑分布式发电机组对电网的影响，强调发电机组应积极采用有功功率控制和无功电压调节技术，主动参与电网的调度运行。基于上述分析讨论了主动配电网的技术实现，包括规划运行一体化的规划技术、充分考虑高渗透率光伏发电接入的运行控制技术、鼓励用户积极参与节能减排的需求侧响应技术和分布式可再生能源的功率控制技术。

... 0 引言随着分布式发电(Distributed Generation,DG)技术的成熟,使得DG的应用得到巨大推广,合理容量的DG并网能够降低系统损耗,改善电能质量以及提高系统可控性^[1,2,3] ...

2016

0.0

2015

0.0

2019

0.0

... 目前,国内对于含DG配电网的主要研究放在供电质量、可靠性、继电保护以及DG的规划上^[4,5,6],在经济性调度上还有所欠缺 ...

2019

0.0

... 目前,国内对于含DG配电网的主要研究放在供电质量、可靠性、继电保护以及DG的规划上^[4,5,6],在经济性调度上还有所欠缺 ...

2018

0.0

... 目前,国内对于含DG配电网的主要研究放在供电质量、可靠性、继电保护以及DG的规划上^[4,5,6],在经济性调度上还有所欠缺 ...

2018

0.0

... 文献[7]针对#cod#x0201c ...

2016

0.0

... 文献[8]提出了空间和时间尺度全局协调优化的调度模型,通过分布自治、分解协调机制开发了综合优化调度系统 ...

2018

0.0

... 文献[9,10]分别提出日前两阶段及双层优化调度模型,力求达到系统运行经济性最高 ...

2016

0.0

... 文献[9,10]分别提出日前两阶段及双层优化调度模型,力求达到系统运行经济性最高 ...

2011

0.0

... 文献[11,12]通过需求侧响应来降低用电成本 ...

2012

0.0

... 文献[11,12]通过需求侧响应来降低用电成本 ...

2018

0.0

... 文献[13,14]通过网络重构来使调度模型经济性达到最高 ...

2015

0.0

... 文献[13,14]通过网络重构来使调度模型经济性达到最高 ...

2019

0.0

... 文献[15]提出一种动态-遗传算法的混合储能系统实时协调调度方案,能够对调度方案进行实时修正,但其实时修正阶段采用储能系统进行柔性控制,使电网投资成本加大 ...

2014

0.0

唐聪岚, 卢继平, 谢应昭, 等. 基于改进数据流在线分割的超短期负荷预测[J]. 电网技术, 2014, 38(7): 2014-2020.

To improve both realtime performance and accuracy of ultra short-term load forecasting and to cope with the higher requirement of power grid on realtime load forecasting, based on improved data stream on-line segmentation an ultra short-term load forecasting method is proposed. Based on the time trend of load development, the realtime data stream processing is utilized in the proposed method to perform ultra short-term forecasting, then combining with the results of short-term load forecasting, which contain the whether factors and the effect of load cycle property, the realtime forecasting result at the segmentation point is corrected. The fast segmentation and forecasting ability of the proposed method avoid repeat modeling and improve the speed of forecasting; the realtime correction and handling of the segmentation point increase historical information utilization and decrease the error of segmentation point, thus the forecasting accuracy can be maintained at a better level. Actual load data is adopted to validate the effectiveness of the proposed model, and validation results show that both load forecasting accuracy and speed by the proposed model have an advantage over those by several conventional ultra short-term load forecasting algorithms, besides the forecasting error at the inflection point of load can be decreased and the proposed method can also adapt to the sudden change of the weather.

State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Shapingba District, Chongqing 400044, China

为同时提高超短期负荷预测的实时性和准确性,应对现代电力系统对实时负荷预测的更高要求,提出一种基于改进数据流在线分割的超短期负荷预测方法。该方法根据负荷发展的时间趋势,利用数据流实时处理技术进行超短期预测,然后结合蕴含天气因素和负荷周期特性作用的短期负荷预测结果,对分割点的实时预测结果进行修正;其快速分段预测能力,避免了重复建模,提高了预测速度;对分割点的实时修正处理有效地增加了历史信息利用率,降低了分割点误差,使预测精度稳定在一个较高的水平。采用实际负荷数据检验该预测模型的有效性,结果表明,基于该模型的预测精度和速度均优于几种常规超短期预测算法,同时降低了拐点预测误差,在天气突变时也具有稳定的适应性。

... 本文采用基于改进数据流在线分割的超短期预测^[16]对风、光出力及负荷情况进行超短期预测 ...

2015

0.0

马迎东, 王文栋, 温强. 基于混沌搜索策略蝙蝠算法的输电网规划[J]. 电力系统保护与控制, 2015, 43(15): 17-21.

... 1 二进制混沌蝙蝠优化算法本文采用混沌蝙蝠算法^[17]对模型进行求解 ...

2018

0.0

... 储能系统主要在常规负荷处于低位时进行充电,在用电高峰期进行放电,从而起到削峰填谷作用^[18] ...