光伏系统由大量光伏组件串并联而成, 恶劣的工作环境使得系统老化加速^{[1, 2]}。光伏组件之间存在的大量连接设备, 一旦老化产生缝隙, 上百伏的电压就可以将空气击穿, 产生电弧。这种持续的放电现象具有足以引起火灾的极高温度。为此, 许多国家制定了直流电弧检测要求。美国国家电气规范NEC(National Electrical Code, NEC)第690.11号文件要求光伏并网系统直流母线大于80 V的必须具有电弧处理能力。

由于电弧物理过程复杂, 涉及电、热、磁等多个学科, 至今仍没有完备的理论和精确的数学模型^[3]。在电弧故障诊断中, 相对于系统本身特性来说, 往往更关注电弧故障前后特征参数的变化。因此, 目前在处理电弧故障时仍然采用黑箱模型, 分析电弧故障外部特性, 尤其是结合电弧故障诊断理论对故障电流或电压的分析^{[4, 5]}。

在汽车、船舶、飞机等直流系统中已经有许多电弧故障检测的文献^[6]。Naidu M等通过检测电流瞬时变化率检测汽车系统中的串联和并联电弧故障^[7], 但是在系统启停等过渡状态时极有可能造成误动作。Momoh J A等使用傅里叶分解得到信号频谱并利用神经网络判断是否发生故障^[8], 但傅里叶分析为了结果精确要求原始数据长度N尽可能的大, 若将傅里叶分析得到的N/2个数据输入到神经网络显然太过复杂, 同时神经网络需要大量数据训练, 实现难度大。姚秀等研究了电极材料、电弧间距对于电弧特性的影响, 并提出利用电流峰峰值作为时域特征, 频域固定频带能量作为频域特征的多判据检测方法。该方法虽然综合了电弧故障时频域特征, 但依然是简单的固定阈值法, 不能自动校正参数, 且无法解决并网逆变器开关频率噪声干扰问题^{[9, 10, 11, 12]}。文献[13]提出利用滤波器和统计方法计算信号混乱程度来判别故障。光伏系统中电弧特性相对于传统直流系统又有其自生特点^[14], 在实际光伏系统中, 实时变化的光照、逆变器的工作状态都会影响电流波动, 因此该方法也不适用于光伏系统。

此外, 美国圣地亚国家实验室和伊顿公司进行了许多测试工作, 并对常见电弧故障检测算法进行了测试, 结果显示目前许多算法还存在缺陷^{[15, 16, 17, 18]}。Strobl C等通过对实际故障系统正常和故障数据的分析, 得出了许多电弧电流时频域特性并与许多光伏系统暂态过程进行对比, 指出了提高电弧故障检测正确率的关键问题, 但是目前还未提出可行方法^{[19, 20, 21]}。

综上, 目前直流电弧故障的检测方法只提取了故障电弧信号的部分故障特征, 也没有考虑到光伏系统的特点, 造成在某些情况下的误判和漏判, 导致严重后果。本文在分析了光伏系统中电弧故障的特点, 总结传统直流系统电弧故障检测方法各自缺点后, 提出了利用小波包分析和统计分析构建系统特征平面进行判别的电弧故障检测方法。最后仿真及试验证明该方法准确率高, 可以消除逆变器开关频率的干扰。

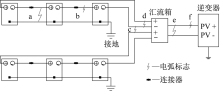
光伏系统中常见电弧故障发生位置如图1所示。光伏组件之间通常使用连接器连接; 连接器老化或者松动产生缝隙是造成串联电弧故障的重要原因之一; 此外, 人为或外部原因造成的传输线损坏也经常导致串联电弧故障发生; 汇流箱与逆变器之间母线由于电压高、电流大也极容易发生并联电弧故障。为确保安全, 大型光伏电站中每块光伏组件一般都需要接地。接地线与光伏组件传输线之间也会由于较大的电势差而产生并联电弧故障。

图1

	Figure Option ViewDownloadNew Window
	图1 光伏系统中常见电弧发生位置

光伏系统中不同位置的电弧故障及常见原因如表1所示。文献[22]根据相关国际标准提出了光伏系统电弧能量的计算方式, 根据该能量大小, 将电弧危害分成大、中、小3种。同时将不同位置发生电弧的概率分成大、中、小三等级。电弧故障类型主要有并联电弧故障和串联电弧故障两种。并联电弧故障的回路电流一般会有明显的变化, 现有的保护断路器已经具备了隔离保护能力; 串联电弧故障, 因受到线路负载的限制, 其回路电流的有效值往往会与负载正常工作回路电流的有效值非常接近, 传统保护方法无法有效实现对串联电弧故障的隔离保护, 进而可能引起电气火灾事故, 因此本文主要针对串联电弧故障进行研究。

表1

表1

表1 光伏系列中不同位置的电弧故障及常见原因 类型 名称 原因 概率 危害 a 对地电弧 线缆绝缘损坏 小 小 b 组串内串联电弧 连接器老化 大 大 c 组串间并联电弧 线缆绝缘损坏 小 大 d 组串内并联电弧 线缆绝缘损坏 小 大 e 母线并联电弧 母线绝缘损坏 中 大 f 母线串联电弧 母线老化 大 大

表1 光伏系列中不同位置的电弧故障及常见原因

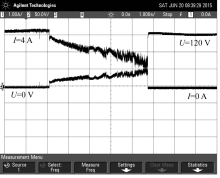
电弧的复杂性和随机性使得目前仍没有完整系统的理论和精确的数学模型描述。针对不同的应用和功率等级, 电弧的近似模型也不同^[23]。在分析电弧故障时, 一般是通过试验采集实际数据再通过函数拟合的方式得到电弧模型。利用4块光伏电池板(光伏组件参数如表2所示), 在光照较大时, 电弧间隙以2.5 mm/s的速度从0增大到10 mm, 测得故障电弧电流电压波形图, 如图2所示。试验开路电压150 V, 负载电流3.2 A, 电弧发生瞬间电流突降, 之后电流线性下降, 最后电流剧烈波动直至电弧熄灭。

表2

表2

表2 光伏组件参数 参 数 数 值 最大功率Pm/W 190 最大功率点电压Um/V 36.67 最大功率点电流Im/A 5.18 开路电压Uoc/V 45.32 短路电流Ish/A 5.53 开路电压温度系数Tv/(%· K-1) -0.356 短路电流温度系数Tt/(%· K-1) +0.024

表2 光伏组件参数

图2

	Figure Option ViewDownloadNew Window
	图2 故障电弧电流电压波形

文献[24, 25]通过光伏阵列不同电压电流等级的试验, 模拟得出的串联电弧数学模型:

uarc=a+bxgap+Udce2αxgape2αxgap+e2αxcrit(1)

式中: u_arc— — 电弧瞬时电压;

a— — 电弧开启电压;

b— — 电压梯度;

x_gap— — 电弧长度;

U_dc— — 直流电压;

x_crit— — 电弧极限长度;

α — — 电压上升斜率。

iarc=Iload-f(b)xgap-Iload(11+e2α(xgap-xcrit))(2)

式中: i_arc— — 电弧电流;

I_load— — 负载电流;

f(b)— — 电流梯度。

虽然不同光伏阵列外在环境变化与文献[24, 25]不完全相同的, 但是建立电弧模型时只需考虑影响电弧的基本要素:电弧长度、直流电压、电弧极限长度、电弧开启电压、电压梯度、电压上升斜率、负载电流和电流梯度。不同的系统和环境影响只是电弧基本要素的取值不同, 电弧的基本模型是不会变的, 因此该模型在工程上适用于不同光伏系统直流故障电弧模拟。

电弧的极限长度x_crit是指当电弧长度大于此值电弧将会熄灭。试验数据显示此极限长度受周围环境参数和电极材料等影响较大, 在恒定电压、电流下, 可认为在某一均值附近随机变化。电弧开启电压a表示电弧产生瞬时的基础电压。试验表明在较大直流电压及电流负载范围内, a均为常数且维持在10~20 V。电压梯度b表示小于极限长度时, 电弧电压随电弧长度线性增加的程度。试验证明该值也在较大范围内保持恒定。电压上升斜率α 表示在电弧长度接近极限长度时, 电弧电压迅速升高的速率。电流梯度与电压梯度呈现固定线性关系。直流电压和负载电流表示系统正常时电源电压以及负载电流。

针对上述模型中具体参数取值, 本文搭建了试验平台, 通过光伏阵列不同输出工况计算获得电弧模型参数。电弧模型参数如表3所示。表3中数据说明, 电弧模型的参数在不同工况下基本保持稳定。使用该参数可以建立近似电弧模型。

表3

表3

表3 电弧模型参数 试验条件 a b α 180 V(3.2 A) 14 10.2 151 130 V(3.2 A) 16 10.4 149 130 V(2.8 A) 14 10.4 156 180 V(2.6 A) 15 10.8 154

表3 电弧模型参数

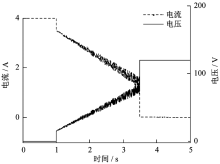
根据式(1)、式(2)以及表3的参数在仿真软件PSIM中建立仿真模型, 仿真时取a=16, b=10.4, α =149。图3为电弧长度以2.5 mm/s匀速增大直至电路完全断开时电弧电压和电流波形图。电弧在1 s 时发生, 在3.5 s时电路完全断开。仿真电路开路电压为120 V, 负载电流为4 A, 与图2相比可以看出该模型与试验数据基本一致。图2中试验电弧燃烧时间比图3仿真略长, 主要是由于试验中电弧两端电压较高, 导致电弧极限长度较长, 燃弧间距增大造成。

图3

	Figure Option ViewDownloadNew Window
	图3 电弧电压电流波形

本文通过小波包分解提取频域特征, 建立基于子频带能量的频域特征向量; 利用方差提取时域统计特征, 建立时域特征向量。频域特征向量之间的距离称为频域距离, 时域向量之间的距离称为时域距离, 时、频域距离一起构成系统特征平面。最后根据系统特征平面中的位置实现电弧故障检测。该方法综合了信号的时域、频域信息, 对电弧故障特征的提取较为全面, 同时结果还表明该方法可以除去逆变器开关频率的干扰。

2.1 特征向量提取

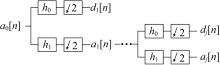
由于故障信号大多为非平稳信号, 小波分析相对于传统的傅里叶分析更加适用于电弧故障检测^{[26, 27]}。离散正交小波变换可以通过树状滤波器组实现^{[28, 29]}。离散正交小波分解示意图如图4所示。图4中a₀代表原始数据; h₀和h₁分别代表高通和低通滤波器系数; a_j和d_j分别代表小波分解第j层的近似系数和细节系数。

图4

	Figure Option ViewDownloadNew Window
	图4 离散正交小波分解示意图

设信号长度为N, 滤波器长度为K, 则第j层小波变换的近似系数和细节系数分别如式(3)、式(4)所示。由于2倍抽取, 第j层系数的长度为 N2j。

aj[n]=∑k=0K-1aj-1[2n-k]·h1[k](3)dj[n]=∑k=0K-1dj-1[2n-k]·h0[k](4)

通过式(3)、式(4), 小波变换可以将原始信号分解到任意层, 对于每一层小波变换都可以得到近似系数和细节系数。近似系数表示信号的相对低频成分, 细节系数表示信号的相对高频成分。为了得到各个子频带的能量, 使用小波包变换, 即对每层近似信号和细节信号都进行分解。经过j层分解可得到2^j组频带系数。设某频带系数为c_m, 定义该频带能量为

em=cmcTm(5)

式中: cTm— — c_m的转置;

m— — 频带序号。

根据Parseval恒等式(6), 可知时域信号能量等于各频带小波变换系数内积之和。

∑n=0Ns(n)·s(n)=∑m=02i-1∑k=0N1cm(k)·cm(k)(6)

式中: N₁— — c_m的长度。

单独考虑某一频带能量特征容易受到外界干扰。逆变器开关频率及其谐波所占频段能量极大, 不同逆变器可能采用不同开关频率, 由此导致的频带能量漂移也会使得固定频段能量的频域特征提取方式不稳定^{[30, 31]}。本文将各频带能量归一化后一起作为频域特征向量。该特征向量不仅在故障前后变化明显, 同时, 可以抑制不同开关频率造成的频带能量漂移问题, 非常适合用来提取电弧故障的频域特征。频带能量归一化是指将某一频带能量除以所有频带能量之和, 为提高各频带能量差别的分辩率, 对结果采取10的对数, 则

Em=log10em∑m=02j-1em(7)

因此频域特征向量为

F=[E0, E1, E2, …, E2j-1](8)

系统中其他故障以及系统中其他逆变器启停可能产生暂时的高频信号, 使得频域向量做出故障指示。同时, 电弧燃烧过程中受到许多环境因素的干扰, 导致电流非常不稳定, 电流波动幅度大。将这一时域特征通过合适的方法提取可以有效提高故障检测的稳定性。方差表征了信号偏离中心的程度, 故可将电流看成随机变量, 用方差提取电弧故障时域特征。对长度为N的电流i(n), 则时域特征向量为

V=[v](9)

其中,

v=1N∑n=0N-1[i(n)-μ]2μ=1N∑n=0N-1i(n)(10)

2.2 电弧故障识别方法

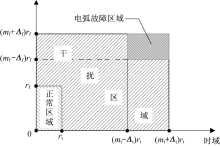
电弧故障诊断中重要的一步是将提取的特征通过合适的分类方法将电弧故障状态与正常状态区分开来。计算频域特征向量与频域原点之间的距离, 得到频域特征距离; 同理可得时域特征距离。利用时域和频域特征距离构建系统特征平面, 如图5所示。根据特征平面中的位置可以确定电弧故障是否发生。

图5

	Figure Option ViewDownloadNew Window
	图5 系统特征平面

未发生电弧故障时, 频域特征距离和时域特征距离均很小, 且在一很小范围内波动。电弧发生之后, 频域特征距离和时域特征距离均增大数倍。图5中, r_f、r_t是正常区域的边界; m_f、Δ _f和m_t、Δ _t分别用于确定电弧故障区域的时域和频域边界。Δ _f和Δ _t决定了电弧故障区域频域和时域的宽度。

在正常区域和故障区域之间, 为干扰区域。系统暂态过程, 如启停、局部阴影时的系统优化等都会造成瞬时的较大电流波动, 但是在频域并不会造成频带能量的大幅偏移。这时判别结果位于图5的右下方。在光伏电站中不同逆变器之间的干扰会导致子阵列直流母线上的电流信号频带能量发生较大变化, 电流幅值却基本不变, 对应于特征平面的左上方位置。实际系统工作电磁环境复杂, 工况变化多, 许多非正常工作状态不能判定为电弧故障。传统检测方法采用二元论, 即非故障即正常的检测分类法, 会导致大量的误判。本文通过建立系统特征平面, 并将其分成正常、电弧故障和干扰(特殊工作状态)3大区域。根据电流信号的分析结果, 实时确定系统状态, 有效降低了电弧故障的误判率, 同时为电弧故障定位提供了思路。

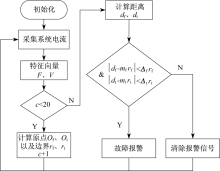
正常状态边界r_f、r_t和系统原点O_f、O_t可通过多次取均值的方法得到。电弧故障判别流程图如图6所示。即循环取原点和特征向量的中点为下次循环的原点, 取边界和特征距离的平均值为下次循环的边界。在线计算出初始原点后, 频域特征距离和时域特征距离分别按式(11)和式(12)计算得到。

$d_{f}=\sqrt{[F-O_{F}]^{2}}$ (11)

$d_{t}=\sqrt{[V-O_{t}]^{2}}$ (12)

图6

	Figure Option ViewDownloadNew Window
	图6 故障判别流程图

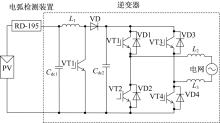
基于上述理论分析, 建立了PSIM仿真模型。PSIM的仿真模型原理图如图7所示。光伏组件参数采用表2的光伏组件参数进行设置。利用PSIM仿真软件中的C Block模块, 并通过非线性元件模块实现仿真所需要的故障电弧模型。逆变器采用双闭环控制, 其参数根据实际光伏逆变器参数进行设置, 其中L₁=2 mH, C_dc1=14 μ F, C_dc2=780 μ F, L₂=L₃=1.4 mH, f=20 kHz。其中逆变器输入电容C_dc1对电弧噪声影响较大, 其值越大越难起弧。仿真所用参数根据某款商业3 kW光伏并网逆变器选取。采用4块相同参数的光伏组件与电弧模块串联后与逆变器相连, 电弧故障发生在直流母线上, 由于4块光伏板串联, 因此电弧故障发生的位置在直流母线上和光伏板之间是一样的。为观察逆变器开关频率对文中方法的影响, 仿真逆变器采用12 kHz、14 kHz、16 kHz、18 kHz、20 kHz的5种不同开关频率。

图7

	Figure Option ViewDownloadNew Window
	图7 PSIM仿真模型原理图

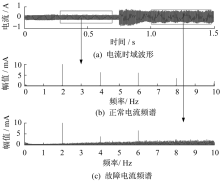
使用前文所述的电弧模型, 在固定距离下产生电弧, 采集电流并滤除直流部分, 可以得到电弧电流时域波形及各部分频谱图, 如图8所示。频谱中因包含逆变器开关频率而存在的开关频率及其整数倍的频率成分, 幅值相对较高。对比正常电流频谱和故障电流频谱可以发现, 正常时电流高频成分很少, 但是故障电流中高频成分显著增多。

图8

	Figure Option ViewDownloadNew Window
	图8 电弧电流时域波形及各部分频谱图

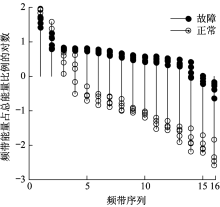
提取正常电流和故障电流频域特征向量F, 频带能量归一化并取对数如图9所示。前3个分量为逆变器开关频率及其谐波所在频段的能量, 这些值均较大且在故障后稍有减少。F后13个分量是系统背景噪声和电弧频率所在频段, 在故障发生后, 电弧所在频段能量显著增大。这表明, 在故障发生之后开关频率及其谐波所在的频段能量往高频区域流动。图9就表明特征向量F可以有效反映故障的频域特征。

图9

	Figure Option ViewDownloadNew Window
	图9 频带能量归一化并取对数

同时, 图9中分别采用5种不同开关频率, 其结果均显示出相同趋势, 即在不同逆变器开关频率下, 该频域特征向量均可以正确反映故障前后频域的变化。

表4为5种不同逆变器开关频率下, 故障电流与正常电流的方差值。表4中数据表明, 电流方差故障时明显比正常时大, 且基本保持稳定。电流幅值的方差可以有效提取故障时域特征。

表4

表4

表4 仿真故障电流与正常电流方差值 开关频率/kHz 方差 类型 12 0.033 8 正常 0.060 1 故障 14 0.029 3 正常 0.056 4 故障 16 0.029 0 正常 0.052 1 故障 18 0.025 8 正常 0.047 5 故障 20 0.022 9 正常 0.044 9 故障

表4 仿真故障电流与正常电流方差值

最后利用96组故障数据和96组正常数据进行故障诊断, 仿真识别结果如图10所示。

图10

	Figure Option ViewDownloadNew Window
	图10 仿真识别结果

图10中区域I为正常状态, 由于正常状态下比较稳定, 因此大多数点都集中在一起; 区域II是电弧故障区域; 剩下的为干扰区域。区域III为模拟逆变器暂态过程以及环境变化时的状态, 此时由于电流变化较大, 导致较大的方差, 然而高频部分仍没有太多变化, 逆变器暂态过程大多为根据光照变化而进行的工作点调整, 由于光照变化较慢, MPPT跟踪周期也较长, 一般不会产生高频震荡噪声, 因此与Ⅱ 区有较高的区分度; 区域IV模拟电站系统中其他子阵列逆变器工作对当前阵列的影响, 此时直流母线电流加入许多高频成分, 频域能量变化较多, 而电流方差却基本不变。由图10可见, 电弧故障区域与正常区域相距较远, 很容易区分, 同时使用合适参数还可以将电弧故障与其他非正常工作状态导致的干扰区分开来, 在仿真当中电弧故障检测的准确率为100%。在频域特征提取过程中, 若采用传统的固定频段能量的方法, 在不同逆变器开关频率下, 系统正常工作时可能会被判别到Ⅱ 区, 增加电弧故障识别难度。

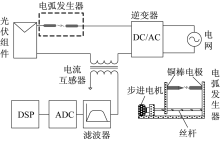
考虑到仿真结果与实际情况的差别, 本文设计了基于DSP的检测系统进行验证。试验依然使用4块表2所示参数的光伏组件。电弧发生器采用步进电机精确控制电极分离的速度和距离。系统用逆变器开关频率为20 kHz。检测系统结构如图11所示。检测板采用高速数-模转换器, 并在采样之前利用上限40 kHz和下限100 kHz截止频率的带通滤波器对原始信号进行了硬件滤波处理。

图11

	Figure Option ViewDownloadNew Window
	图11 系统结构图

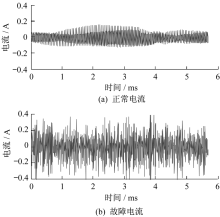
试验中电弧故障诊断运算时间为0.8 ms, 远远低于实际电弧故障处理要求时间, 电弧长度可以认为没有变化。试验时, 首先采集正常状态电流, 然后利用步进电机以1 mm/s速度将电极分离至3 mm距离并固定, 采集故障电流, 时间都是6 ms, 分别采集1 080个数据。试验电流信号如图12所示。由图12可见, 电弧故障发生后, 电流波动显著增大。由于系统有较多暂态过程, 单纯使用电流峰峰值判断是否发生电弧会造成较多误判。采用本文方法可以极大减少由于暂态过程或逆变器开关频率噪声引起的误判问题。

图12

	Figure Option ViewDownloadNew Window
	图12 试验电流信号

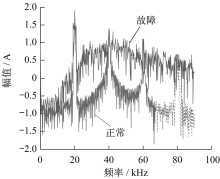
计算正常电流和故障电流频谱, 如图13所示。实际采样频率为180 kHz, 频谱幅值采用10的对数显示。由图13可见, 电弧发生后, 开关频率附近能量占比降低, 开关频率以外频率成分显著增加。

图13

	Figure Option ViewDownloadNew Window
	图13 正常电流和故障电流频谱

与仿真数据相比, 实际电流的频谱分布更加均匀, 即逆变器开关频率及其谐波以外的频率成分也较多, 这是由于试验中电磁环境更加复杂, 而仿真中只有逆变器功率器件开关状态的干扰。图13可见, 电弧电流频谱非常宽, 使用某一固定频段提取频域特征不合理且极易受到干扰。

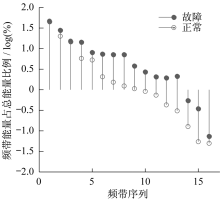
利用前文所述的方法提取频域特征, 即频域特征向量, 实际频带能量分布如图14所示。对比可发现实际情况与理论分析基本一致。频域特征向量后半部分在故障发生前后有显著变化。试验中电磁环境比仿真时复杂许多, 导致能量分布相比仿真更加均衡。以正常状态下为例, 仿真结果表明信号能量基本分布在开关频率所在频段, 其他频段尤其是高频段能量非常小; 而在试验中, 系统除去逆变器开关频率还存在其他干扰信号, 导致信号能量较平均的分布在各频段内, 使得高频段能量相对较大。尽管如此, 图14依然明确表明本文提出的频域特征向量准确的表征了频域特征信息。

图14

	Figure Option ViewDownloadNew Window
	图14 实际频带能量分布

时域特征, 即试验故障电流与正常电流方差值电流幅值的方差如表5所示。其中正常数据和故障数据各3组。由表5可见, 故障前后电流方差相差一个数量级, 比仿真数据更明显。这是因为故障电流的方差主要受环境因素的影响, 环境的细微改变也会造成电弧故障较大波动, 进而导致较大的方差。

表5

表5

表5 试验故障电流与正常电流方差值 序号 方差 类型 1 0.004 8 正常 2 0.005 7 正常 3 0.005 0 正常 4 0.044 5 故障 5 0.046 2 故障 6 0.046 3 故障

表5 试验故障电流与正常电流方差值

最后, 对该系统进行试验验证, 试验采集晴朗气象条件下, 从早晨到傍晚的外界环境变化时正常情况和故障发生时的数据, 涵盖了光照和温度等外在条件变化比较明显的点。试验中只需采样10组数据就可以包括逆变器以及试验环境不同情况下的典型工作点, 试验中共进行20次试验, 其中10次为光伏系统正常稳定工作时检测装置采集系统电流并进行判别; 剩下10次为光伏系统稳定工作, 利用电弧发生装置产生电弧故障时检测装置的判别结果。结果显示20次试验全部可以正确识别, 没有发现误判和漏判现象。

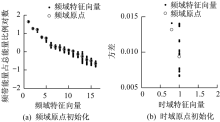
系统初始化过程中检测算法自动寻找到的时频域原点。原点初始化如图15所示。图15中实心原点表示时频域向量初始化所使用的数据, 空心圆圈表示最终寻找到的原点。图15结果表明, 时频域原点均取在了历史数据的中心, 其中历史数据是初始化过程中采集的20组数据, 并默认初始化数据为正常状态, 具有较强代表性。

图15

	Figure Option ViewDownloadNew Window
	图15 原点初始化

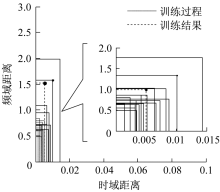
边界训练结果过程和结果如图16所示。图16中虚线为边界初始化的轨迹, 实线为最终初始化结果。根据初始化结果可以确定故障和正常区域。

图16

	Figure Option ViewDownloadNew Window
	图16 边界训练过程和结果

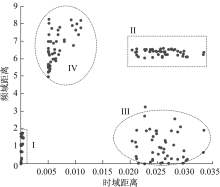
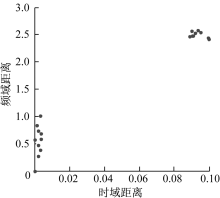
全部20次检测, 试验数据识别结果如图17所示。

图17

	Figure Option ViewDownloadNew Window
	图17 试验数据识别结果

由于在实际试验时, 逆变器电路以及外在试验的环境会有很多不同的噪声, 这些噪声可能会叠加也可能会互相削弱而在仿真过程中无法模拟实际复杂的电磁环境, 因此试验和仿真的结果有一定的差距。由图17可见, 10组正常工作试验的数据全被判别到特征平面的左下角的正常区域, 10组故障实验数据则判别到右上角故障区域, 与此前分析一致。上述试验结果表明, 时-频域特征向量可以有效提取故障特征。基于系统特征平面的故障判别方法可以有效区分故障与正常状态, 说明得到的边界值具有典型性并可以进行推广。

本文考虑到光伏系统中电弧故障的危害以及传统电弧故障检测方法的缺点, 提出了基于系统特征平面的新型检测方法。系统特征平面由频域特征向量之间的距离和时域特征向量之间的距离构成, 频域特征向量使用小波能量分析方法提取, 时域特征向量为电流幅值的方差。频域特征向量可以自动排除逆变器开关频率的干扰, 时域特征向量加强了抗干扰能力。试验和仿真结果表明该方法准确有效, 未出现误判及漏判的情况。